yep - smoothing the spectrum with a lop~ was not a good idea, i assume. and also my convolution with the kernel i used was not a good idea, since it created an offset of the frequencies in the final spectrum. but that smoothing kernel can also be properly represented really symmetrically if half of it is in the negative frequencies (at the end of the array). and i omitted the convolution with tab_conv in favor of frequency domain convolution with vanilla objects which should be quite fast as well:

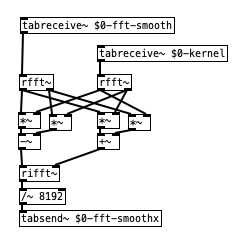
the smoothing kernel in this case is just a 64 sample hann window (split in half). barely visible here - and possibly, it might be a good idea to use an uneven width and offset it. not sure ...

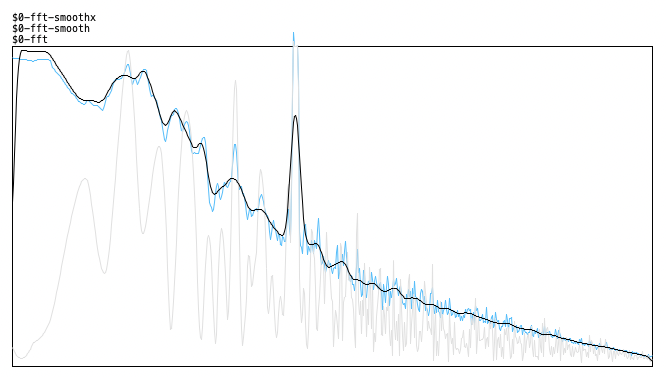
here's the result (original, smoothed values and smoothed spectrum) - looks quite correct. there's a 4000Hz signal peak here besides the pink noise now that makes it more obvious:

@manuels I was not prev aware of these other kinds of white noise but they are all smooth and so don't produce the kind of texture I want. To give you a sense of what I'm looking for, here is the sound of a drip into an empty tin can: tinCanDrip1.wav. Convolved with binary white noise, you get this: tin can conv binary noise.wav. Now here is my nasty-sounding whitening of bubbling water and it's convolution with the tin can: whitened bubbling.wav & tin can conv whitened bubbling.wav. See how the result sounds a little like a small stone being rolled around the bottom of the can?

Also, that's interesting about [noise~] in overlapped windows, I'll go back and modify my version of that patch to see if the lo-fi mp3 quality goes away.

@whale-av "randomly modulated in its amplitude"--yes, that's what I tried with the 64 band 1/5 oct graphic. It's not bad, but it's not natural sounding either. Could be useful anyway, depending on the effect you want.

@ddw_music My problem isn't the convolution (I'm using REAPER's ReaVerb for that), I'm just wondering how to make the kind of IR that produces the effect I want. Your rifft strategy is what I speculated about in my original post and what I first tried using [array random] to generate freq domain moduli with a similar distribution as [noise~]. FYI Pd's real inverse FFT automatically fills in the complex conjugates for the bins above Nyquist, so you don't have to write them--leaving them as all 0 is fine. Also note that your [lop~] is filtering the change between successive bin moduli in a single window, not the change of each bin from window to window. I'm speculating that the latter (maybe using asymmetric slewing rather than low pass filtering) would make frequency peaks hang around longer (and hence more audible) whereas I'm not sure what the former does. That said I think the strategy of modifying natural sound is paying off faster than these more technical methods.

@jameslo said:

This may be complete BS, but here goes: when I convolve a 1s piano chord sample with 30s of stereo white noise, I get 30s of something that almost sounds like it's bubbling, like the pianist is wiggling their fingers and restriking random notes in the chord (what's the musical term for that? tremolo?). It's not a smooth smear like a reverb freeze might be.

If you are just doing two STFTs, sig --> rfft~ and noise --> rfft~, and complex-multiplying, then this is not the same as convolution against a 30-second kernel.

30-second convolution would require FFTs with size = nextPowerOfTwo(48000 * 30) = 2097152. If you do that, you would get a smooth smear. [block~ 2097152] is likely to be impractical. "Partitioned convolution" can get the same effect using typically-sized FFT windows. (SuperCollider has a PartConv.ar UGen -- I tried it on a fixed kernel of 5 seconds of white noise, and indeed, it does sound like a reverb freeze.) Here's a paper -- most of this paper is about low-level implementation strategies and wouldn't be relevant to Pd. But the first couple of pages are a good explanation of the concept of partitioned convolution, in terms that could be implemented in Pd.

(Partitioned convolution will produce a smoother result, which isn't what you wanted -- this is mainly to explain why a short-term complex multiply doesn't sound like longer-term convolution.)

If I'm right, I think I should be able to increase the bubbling effect by increasing the volume variation of each frequency and/or making the rate of volume variation change more slowly.

Perhaps... it turns out that you can generate white noise by generating random amplitudes and phases for the partials.

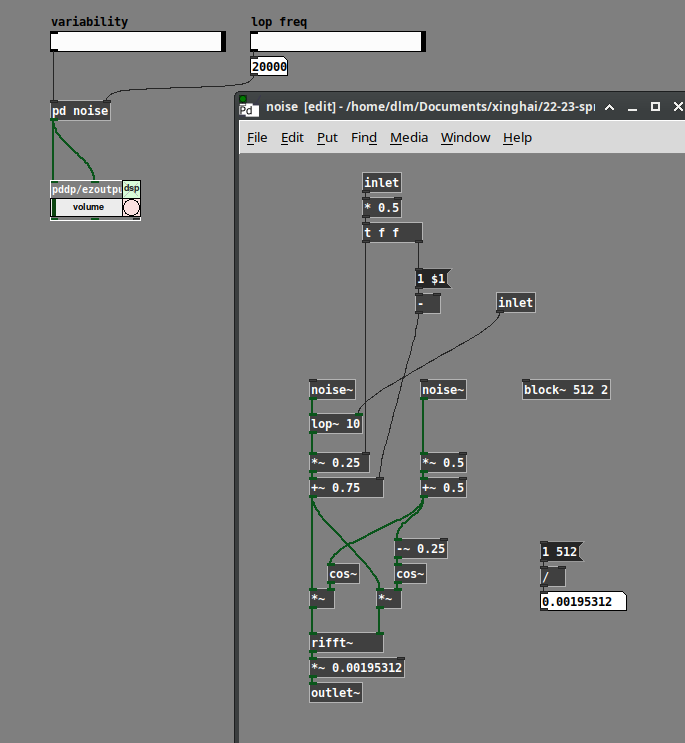
(One thing that is not correct is that the upper half of an FFT frame is supposed to be the complex conjugate of a mirror image of the lower half: except for bins 0 and Nyquist, real(j) = real(size - j) and imag(j) = -imag(size - j). I haven't done that here, so it's quite likely that the non-mirrored mirror image neutralizes the control over randomness in the magnitudes. But I'm not that interested in this problem, so I'm not going to take it further right now.)

[lop~] here was a crude attempt to slow down the rate of change. (Note that I'm generating polar coordinates first, then converting to Cartesian for rifft~. The left-hand side is magnitude, so the lop~ is here but not affecting phase.) It doesn't make that much difference, though, if the phases are fully randomized. If you reduce the randomization of the phases, then the FFT windows acquire more periodicity, and you hear a pitch related to the window rate.

Anyway, perhaps some of this could be tweaked for your purpose.

hjh

@ddw_music said:

estimating filter parameters from a sampled frequency response

That's probably how I should have asked my question because that's really the issue. It's easy enough to get the freq response of a filter characterized by an impulse response, so the convolution stuff I mentioned is just a distraction (i.e. an old guy telling war stories ).

@lacuna said:

Just guessing here: Convolution backwards is deconvolution, isn't it?
... but the whole topic of resynthesis is very broad and diverse, - plus a filter could be virtually anything.

It's not convolution that I want to invert (see comment above about distraction ). But you're right to point out how amorphous my question is. I thought maybe the kind of sound I'm interested in is so constrained that filter model would be simple (e.g. just a bunch of [vcf~]s in a row).

@ddw_music said:

Another technique is Linear Predictive Coding

Is there a tool you would recommend?

@whale-av Again, convolution is probably a red herring. I don't recall ever getting [partconv~] (bsaylor) to work but I've definitely rolled my own convolution using a delay line and a clone for every sample in one of the vectors (!). Optimization is the enemy of fun

@jameslo I don't have an answer to the main question. I suspect it would be tricky, since the most common filters are second-order IIRs, while sampling an impulse response is a high-order FIR.

The Dodge/Jerse Computer Music book discusses sampled frequency responses. Effectively, if you plot out a desired gain per bin and do an inverse cosine transform on it, then you get an impulse response. For an FIR, the impulse response is the same as the coefficients. But it may be more efficient to resample the frequency response -- keep it in the frequency domain and do FFT multiplication. I guess it depends on how many bins you have. 30-50 bins, maybe brute force multiply-add might be faster? (At least in SC, Nick Collins' LTI Linear Time-Invariant unit might be faster for relatively short kernels.) A thousand bins, definitely FFT would be faster.

I should check the book, see if they have any ideas about estimating filter parameters from a sampled frequency response. But I don't recall that they take it in that direction.

A fun observation here is -- since you can do filtering by convolution, and you can also do reverb by convolution, then reverb is a special case of filtering. I'm overstating for dramatic effect, but... a typical filter's frequency response is smooth and predictable while a reverb's frequency response is irregular and noisy, even with the same mathematical process.

hjh

I think you have to reverse the two inputs of pd fft-convolution.
ir-convolution-Modif.zip

http://www.pd-tutorial.com/english/ch03s08.html
This is a convolution patch based on this site with pd-extented, but it sounds the same between both ears. Please tell me what is wrong.
Also, if you have a sample patch about this, please let me know.

IR-convolution.zip

@Laevatein do you want to avoid externals in general?

my spoonful of wisdom if you want to do something like earplug~ with pd-vanilla objects only:

First you'll have to figure out how to do the panning between your channels. basically you have two options, vbap (vector based amplitude panning, read: https://ccrma.stanford.edu/workshops/gaffta2010/spatialsound/topics/amplitude_panning/materials/vbap.pdf) or dbap (distance based amplitude panning, read http://www.pnek.org/wp-content/uploads/2010/04/icmc2009-dbap.pdf).
Actually it's just triangulation, not too complicated stuff. You'll find many open source code examples online, including pd-patches, e.g. [pan8~] in the else library or my humble implementation [pp.spat8~] in audiolab are dbap. Both are available in the deken repos (help -> find externals)

The convolution part is a bit more complicated. You can do it in pd-vanilla, there are some examples in Alexandre Torres Porres live electronics tutorial, which is now part of the else library i think. But if you care about latency or if your IR files are larger than a few hundred milliseconds you'll have to use partitioning. Again, you can find examples online. Tom Erbe shared something a few years ago, there are patches in else, in audiolab ... Problem is though if you're doing the convolution part in pure data and you'll need to convolve with say 8-16 stereo impulse responses to get a decent binaural effect... it will bring your modern day computer to it's knees. You can try to outsource the convolution part to different instances of pd with [pd~] but I think it makes much more sense to do it with tools that are better suited for this task. jconvolver comes to mind if you're using jack.
good luck with your project!

(edit: grammar)

@jancsika timbreID neat external by William Brent:
This is a collection of audio feature analysis externals for [Pd]. The classification extern (timbreID) accepts arbitrary lists of features and attempts to find the best match between an input feature and previously stored instances of training data.
http://williambrent.conflations.com/pagez/research.html

Code:
https://github.com/wbrent/timbreID

Video demo:
http://williambrent.conflations.com/mov/timbre-space-june-2019.mp4

Hi guys,

I'm trying to vocalize a whisper speech using fft convolution; starting from two distinct inputs <a sampled vocal and a whisper speech> I have seen that is possible to generate a sort of vocal/normal speech.

I wonder if is there a way to improve the quality of the convolution process so that the result will sound more similar to the input vocal timbre than it is now.

Thanks in advance.
wts.zip