@raynovich Did you try increasing the delay in your audio interface settings? On one of my patches that fixes the drop out after I create and destroy the gem window once.

I just got a fast new computer and I get a very short dropout on [create( but not [destroy(, so I guess that means "yes, that's just the way it is"?

I wonder if you put the GEM stuff in another process (using [pd~]) and you didn't return any audio from that process whether that would address this issue? EDIT: nope, it doesn't. And launching the subprocess is even more disruptive.

@rewindForward In addition to sharing your patch (it could even be one using [expr~]), please let us know what your trigger signal is (i.e. I'm unclear why the signal is ~1 ms long)

@whale-av I thought I had figured out the relationship between Q and BW but my patch failed miserably. So I just went with BW but got the same "close but no cigar" results:

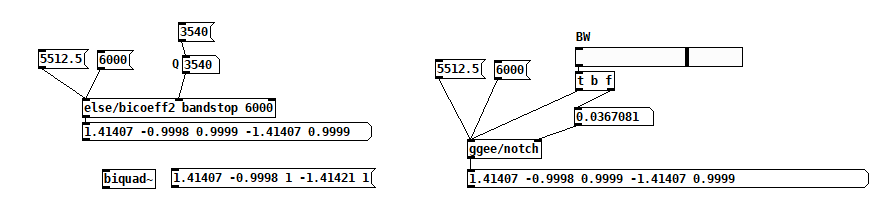
Edit: looking back at that cookbook formula for notch coefficients (https://webaudio.github.io/Audio-EQ-Cookbook/audio-eq-cookbook.html), ff1 and ff3 are defined as 1/1+alpha, so the only way that could equal 1 is if alpha equals 0. But alpha is defined as sin(2 * pi * f / sr) / 2 * Q, so f would have to be 0 or Nyquist, or else Q is so large that it underflows the precision of the floats used to calculate the coefficients? And if it's the latter, then that seems like a weird thing to present as an illustrative example. (Note that in the example, f = 5512.5 = Nyquist/4--prob not a coincidence)

I'm still mystified.

In the help patch for [biquad~] there are coefficients for a very narrow bandstop filter centered at 5512.5 hz @ 44.1k or 6000 hz @ 48k. The filter's Q isn't stated so I thought I could reverse engineer it using those coefficients as my key but I can't seem to generate them exactly by using either my own coefficient calculator or the one from ELSE (bicoef2). I get close with a Q of about 3500, but I can't match all coefficients with a single Q value (I can't remember if the 1s are even posssible). Why would that be?
help coefficients search.pd

@april Check the order of coefficients to [biquad~]. I think the feedback coefficients come before the feedforward coefficients. Also check the sign of the feedback coefficients. According to this reference https://webaudio.github.io/Audio-EQ-Cookbook/audio-eq-cookbook.html (formula 4) they should be negative.

Edit: additionally, try adding triggers to the outputs of the [expr] objects to ensure each of the sub branches are being evaluated in the order you think they should be. Here's my version based on that reference: biquad notch coefficients.pd

@solipp said:

use [set 64 1 $1(
no need to switch dsp off

OMG, I was staring at my own code and didn't see that!

@hansr If you can tolerate the latency and inflexible cutoff frequencies, I've used FFT resynthesis for this kind of thing. At 44.1 and a window size of 2048, zeroing out the first two bins would get you very close I think. And if I'm not mistaken, doing it this way introduces less phase distortion.

@ddw_music I tested a few of my FFT patches that have adjustable window sizes and they all seem to still work on 0.56.2 without having to cycle dsp off and on. I can confirm that your patch isn't responding though, so maybe there's an issue with the oversampling portion of the message? If I enter your params as arguments in the block~ object, it seems to work fine. Maybe use dynamic patching as a temporary workaround?

@Ice-Ice Well, I was hoping that if I followed that same tutorial I might be able to remedy some of my ignorance of low-level filter construction.

Nope!

But maybe what I made is still useful to you. This is untested because I honestly don't understand what I should be testing for. The examples on that tutorial sound more like feedback delays than all pass filters to me, but that just may be more of my ignorance. That said, my gut tells me that you can't just mashup H14 and this filter diagram--they're slightly different instances of the same thing.
allpass~.pd

Edit: Oooh, I think I see what's going on!
H14 implements the APF using [rzero-rev~] fed into [rpole~]. From help:

    [rzero-rev~] implements y[n] = -a * x[n] + x[n-1]
    [rpole~] implements y[n] = x[n] + a * y[n-1]

Since the first equation provides input to the second, substitute x[n] in the second with the output equation of the first:

    y[n] = -a * x[n] + x[n-1] + a * y[n-1]

Now make an equation for that tutorial's diagram:

    y[n] = -g * x[n] + x[n-M1] + g * y[n-M1]

The first term represents the upper path, the second term is the middle path through the delay, and the last term is the feedback going through the same delay!

So H14 is the same only if a = g and M1 = 1.