@seed said:

small paul
http://www.martin-brinkmann.de/pd-patches.html
there is also one in the DIY2 collection which i think is based off the phase voc
http://pdpatchrepo.info/patches/patch/76

extra
http://williambrent.conflations.com/pages/research.html

Seed, thanks for your reply. I apologize for not acknowleding it sooner, but I've been sick lately.

The small paul has a metallic/reverby sound with rhythmically regular spectrum shifts.

The DIY2 pack includes [smp-timestretch1] and [smp-timestretch2] which seem to be almost identical. They produce an immediately audible rhythmic repetition effect, that is, of a part of the file being looped.

Mr. Brent's [streamStretch] has a sound that is stabler than the others and whose fluctuations are less regular. In nonetheless retains a distinct trashiness (metallic, static-like) when compared to the original sample. Also, it does eventually stop if you set the speed range to "1 1" ("0 0" doesn't seem to do anything), so it's not an infinite stretch.

Any other suggestions are welcome. Again, I merely want to extend the content of a sample like this without a) creating a clear looping rhythm losing the sound quality of the sample. This seems to be quite difficult though.

testbass.wav

@Pierre-Guillot "the Pure data subdirectory is invalid " ? how is this possible, never heard of an invalid directory
oh my god the horror, the horror

Hi all,

Here is a simple piano roll abstraction that someone may find useful:

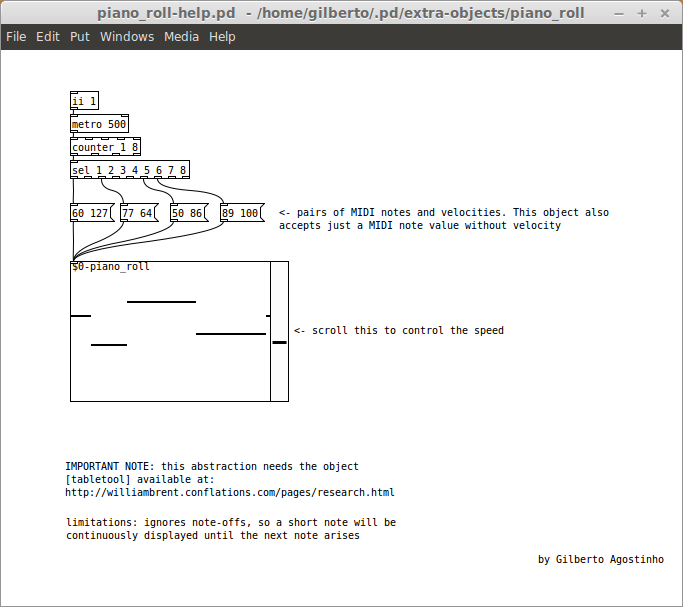
It requires the object [tabletool] from http://williambrent.conflations.com/pages/research.html

Works with both pd-extended and pd-l2Ork. Available at: https://github.com/gilbertohasnofb/pd-abstractions-and-libraries

Cheers,
Gilberto

@dgd There has obviously been a lot of discussion about filters for Pd, latency versus processing overhead, minimum phase etc.
@Katjav is your guru, and I can do no better than to point you here........... http://forum.pdpatchrepo.info/topic/5786/low-latency-fir-filters-minimum-phase-and-partitioned-convolution
Follow the links in that thread.........
David.

Hello Katjav,

I have been chasing the swept sine technique with Farina's Aurora tools on the Cool Edit/Adobe Audition platform. I too found that octave extension of low frequency side only to use as fade in made possible much better result. Also small fade out at the end for non zero end state and all was greatly improved. But applied to getting IR of sound card loopback produces wrong answer. AC coupling of output and input stages produces min phase Butterworth type answer and swept sine with fades always contaminates with its sinc like IR. MLS gives correct answer, but of course brings its own baggage.

Your webpage: http://www.katjaas.nl/expochirp/expochirp.html shows IR result that I've seen on many of my screens while working on the fade issue. Very nicely done indeed.

Farina released plugins for Audacity for convolution and sweep generation. Audacity display doesn't provide zoom tools for display of fine detail. The plugins do provide ready reference.

The solution to the fade issue is to not use them in producing the sweep pair. The answer is in generating at least one of the sweeps in the frequency domain.

Here is link to a great paper covering some of this: "Transfer Function Measurement with Sweeps," SWEN MÜLLER and PAULO MASSARANI I found it here: http://www.melaudia.net/zdoc/comparisonMesure.PDF

Chapter 5 has got the goods.

Turns out that Kirkeby inverse is perfect tool for the job, and many more! To bad it is trapped in Cool Edit/Audition domain. Perhaps Farina will liberate it soon. The perfect place to apply it is before all the trouble begins. An arbitrary broadband signal of 2^n length may be inverted with Kirkeby, and convolution of the pair returns extremely good result. Samples directly next to pulse of 1e-6 easy to obtain. Starting with white noise, results emulating MLS are possible. Starting with exponential sweep a sweep is returned by Kirkeby with circular convolution properties: To get right convolution result, two copies of forward sweep need to be used and cropped to central result. Alternately Kirkeby may be directed to return result 4x longer for direct convolution. I found that a 2x long Kirkeby result produced artifacts. One may also use 2 copies of a 1x Kirkeby to recover IR with single instance of the seed wave.

I communicated this with Farina, and he honored me by placing his confirmations to: http://pcfarina.eng.unipr.it/Public/Wolkoff/

There are six wave files: 2^20 sample length forward sweep and inverse sweep generated without fades; and 1x,2x,4x Kirkeby inverses of the forward sweep. Additionally a time shift Kirkeby is posted. This is a hack I proposed as a partial work around for straight convolution. It is simply cutting first half of 1x Kirkeby and pasting it back at the end. Fading the ends controls bandwidth, and provides kernel for auralization applications.

Cheers!

Check out William Brent's DIlib here:

http://williambrent.conflations.com/pages/research.html

He has it all working pretty smoothly, I've only just started working with his patches so I can't really help you with specifics of tracking multiple users yet. But I thought these patches might help.

Hi Guys,
I was referred to this thread by Serafino Di Rosario, and I will test this PD patch for performing ESS measurements. Everything is very interesting for me, and it seems that Katja did a very good job!

Regarding the problems encountered, I give you these infos:

1. sine-phase-matched sweep. This method is very useful when performing distortion measurements, or computing multiple-order IRS to be used in not-linear convolution processor (for emulating the nonlinearities of a device). For the method to work, it is mandatory that the sine sweep is sine-phased not only at the beginning, but also at the end of each octave. This way, each harmonic-order IR will be phase matched with the linear IR. The provided formulation solves this problem, and it is very good to see it explained here so simply.
   The importance of using a phase-synced exponential sweep was first discovered by Antonin Novak, a Ph.D. student of the universities of Prague and Le Mans.

2. The ripple at low frequencies can be controlled by proper fade-in. The choice of the "optimal" fade law is still a big subject under scientific discussion. Hann windowing is just a very initial, suboptimal approach. I plan to investigate further the choice of the optimal fade law, and publish something on this topic, soon.

3. The concept of cutting away everything before the arrival of the direct sound is wrong, in my opinion. The "silence" before the arrival of the direct sound has a very important physical meaning, it is the "time-of-flight" of the sound, and provides an accurate measurement of the distance between the source and the receiver. Furthermore, it contains "background noise", which is a very important quantity to know, for example when deriving STI from the IR measurement.
   So PLEASE, do not cut away this initial silence! If the IR has to be used as a filter for a convolution-based reverb plugin, the plugin must be intelligent enough for analyzing the IR, and giving the user the possibility to keep this initial silence or cut it away. For example, IR-1 from Waves gives these possibilities. In any case, a measured IR of a room should always contain the time-of-flight... Publishing "pre-cutted" IRs is wrong, and in the long run will cause a lot of troubles...

4. The "Fractional delay", for the same reasons, should NOT be corrected! If the time-of-flight is fractional, good, let's stay with this fact. As pointed out, cutting (time-shifting) improperly the measured IR can alter its spectrum. So, please, keep every measured IR as it comes out from the convolution with the inverse sweep... If the higher-order distortion products are not needed, it make sense to only keep the linear part only, but always starting from the true "zero time". Let's make an example: I generate a 20s-long IR at 48 kHz, that is 960,000 samples.
   The inverse sweep will also be 960,000 samples long.
   I play the sweep, and record the room response for, say, 1,200,000 samples, for being sure of capturing the complete reverberant tail even at the higher frequencies.
   Now I convolve the recorded signal (1,200,000 samples) with the inverse sweep (960,000 samples), and I get a convolved signal which is long 2,159,999 samples.
   If I want to keep a 4s long IR, containing only the linear response, you should throw away the first 959,999 samples, and keep the following 192,000 samples.
   As this signal starts from the true "zero time", the main peak will not be at the very beginning, but delayed of an amount corresponding to the source-receiver distance. If it was 10m, it will be 10/340=0.0294 seconds...

5. For performing efficiently convolution of very long filters (in the example above, the Inverse Sweep was nearly 1 million points) it is advisable to employ a partitioned convolution scheme. That is, the filter is splitted in a number of blocks, so that instead of performing a single, very long FFT , a number of shorter FFTs is performed instead. On my web site you find a couple of papers explaining the partitioned convolution algorithm. This is the same algorithm employed in the well-known BruteFIR open-source program by Anders Torger.

Bye!

Angelo Farina

Convolution in time domain is multiplication in frequency domain, that is, complex multiplication of the real and imaginary parts in signal spectrum and filter spectrum. If the filter is not strictly zero-phase, the multiplication involves phase shifts, and the output signal will be longer than the input. To avoid fold-over of signal samples (circular convolution), techniques of zero-padding and overlap-save or overlap-scrap are normally implemented for fast convolution. It is even possible to cut the impulse response in parts if it is longer than a reasonable FFT size. In another thread, bassik has pointed to this article describing partitioned convolution:

http://www.acoustics.net/objects/pdf/article_farina04.pdf

It is a very interesting technique because, when the filter is causal, low latency processing can be done even with long FIR filters.

I am not sure if fast convolution can be implemented as a Pd patch, because of the required zero-padding. Partitioned convolution is even more complicated. Fortunately, Ben Saylor has written [partconv~], which is in Pd extended. This object can do it all.

Katja

hey, im trying to create a convolution patch in pd for a project.
im trying to use one fft for the impulse response and one for the source material. the aim is to pre load the impulse response through the fft then save the real and imaginary components in 2 tables.
the problem im then having is how to then combine this with the source material in the same way that any convolution reverb works.
thanks

@katjav said:

Hi Bassik,

These comparisons look quite promising! And this is done with the old wiggly chirp. The low frequency ripples over which I'm cracking my brains hardly play a role because the system's response starts at around 100 Hz. I'm curious, what is actually the system under test?

Katja

Hello Katja,

the system under test is a big exhibition hall in london (http://www.vam.ac.uk/collections/fashion/galleries/40/index.html) measured using a genelec 8030A monitor and an omni directional mic only.

Keeping it simple to understand teh results quicker.

Regarding your exp chirp computation, I am afraid this goes above my current knowledge so I need to study a bit before giving you an answer or even a comment.

But we should bear in mind that exp Sweep sine technique is done for measuring acoustic spaces (hence the storing of non linearities of the reproduction and recording system in the anti casual part of the IR) and to obtain high quality IR for convolution and auralisation use.

In this case I don't really get the point why you are researching the exact sample value of the peak value.
In my experience, analysis of simple IR don't give substantial different results if the time zero of the IR is not exactly on the peak but probably I am missing something here expecially regarding the signal processing.

base of the exponentianl or logaritmic sweep is that the instantaneous frequency vary exponentially with time (see http://www.acoustics.net/objects/pdf/article_farina02.pdf)
Hope this can be of help.

Also Farina described a method for fast convolution for ambiophonics that can maybe be of inspiration for the deconvolution engine (see http://www.acoustics.net/objects/pdf/article_farina04.pdf)

Regarding STI, it is a measure of the speech intelligibility in a given space and takes into account many factors of which th emost important are the S/N ratio and the frequency masking.

Voice is a very complex mathematical beast as it has a characteristics frequency respone that vary with spl and also a frequency modulation mechanism that we use to articulate words. this is obvioulsy different for different languags but has been standardised in a certain way.

I will send to you the ISO standard that clearly explains th emethod of calculation impplemented in any commercial software in teh next days.

Also I would like to discuss possible development after the chirp issues are resolved.

I believe that it can be useful to implent the following in the patch:

• Sound editor to delete the anti casual part of the IR and move the arrival time of the peak to zero

• Room acoustics parameters calculation (I will send you the relative ISO and I will write more info later)

• Multichannel IR recording and processing including an Ambisonics module; IEM in Gratz (http://iem.at/Members/noisternig/bin_ambi) has done a great work on this. Our implementation would be much simpler and would include A-format to B-Format encoding and additional analysis.

Hope everything is well in life in the meantime

speak to you soon

Bassik