In Pd of course, anyone?

@ben.wes Beat me to it...
David.

@ben.wes just fyi, * is more efficient than /
I believe pow is less efficient than either but haven't checked

@seb-harmonik.ar said:

* is more efficient than /

yep, that's certainly true, thanks! - had measured this in the past as well (and commented above). i was just naively thinking that it might make a difference whether the argument is an int or float (which is the case for pow ... [pow 2] is faster than [pow 2.01] for example). but this thought doesn't make any sense here.

I think some of these have the same issue as my original implementation - if the generated random phase is less than a sample increment and the phase wraps around it will never be bumped to above 1.
e.g. at 1/4 sample rate samples would be 0, 0.25, 0.5, and 0.75. if generated random value is >=0 and < 0.25 no value will go above 1
edit: @ben.wes not sure but everything in pd is a float
edit2: similarly we have to think about cases where random phase is between 1-(sample increment) and 1. Because it could bump the generated values to always be above 1 in cases where the phase wrap around of phasor~ doesn't start at 0. (in which case there would be no transition either)

@seb-harmonik.ar said:

if the generated random phase is less than a sample increment and the phase wraps around, it will never be bumped to above 1

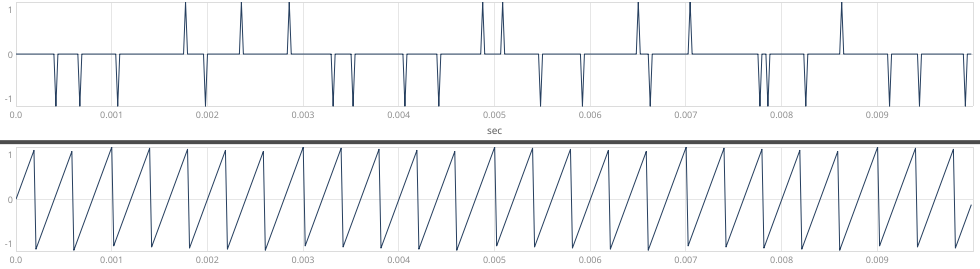
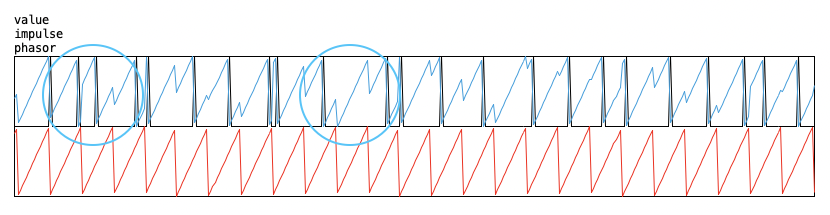
certainly true in my case, yes - there are missing impulses:

@ben.wes As I understand velvet there have to be missing impulses as it should be more sparsely populated than white noise. It's a question of how sparse maybe, but certainly that the sparseness cannot be regular and produce a psychoacoustic audible tone......
.... maybe....
David.

an audible tone would come from period regularity. As I see it it must have an impulse at each period indeed. Haven't tested my patch like that, could you do that too @ben.wes?

@whale-av the version in the paper that this is based on has one impulse every period, randomly distributed somewhere within it.

@porres in my version I added controls for period regularity and polarity bias.
Setting period regularity to '0' constrains the random phase range and polarity bias controls the offset of the noise that chooses the polarity (copysign)
so if you set the regularity to 0 and polarity bias to 1 you get a (aliased) regular pulse train

@seb-harmonik.ar said:

@porres in my version I added controls for period regularity and polarity bias.
Setting period regularity to '0' constrains the random phase range and polarity bias controls the offset of the noise that chooses the polarity (copysign)
so if you set the regularity to 0 and polarity bias to 1 you get a (aliased) regular pulse train

I did not get any of this sorry... what is any of it good for? can you try and ellaborate?

you mean like you can choose how much of it is positive or negative?

that'd be easy with the probability parameter of [chance~] but I don't see any benefit in that.

@porres said:

[...] Haven't tested my patch like that, could you do that too @ben.wes?

... since it's based on the same logic of the randomly offset phasor crossing 1, it also sometimes misses impulses, yes (checked with ~3000Hz):

as far as i can see, all versions here potentially drop impulses? feels like this shouldn't be hard to solve - but i don't see how, i admit. and i probably also should check the previous versions in more detail to really understand them!

another simple approach is this, where i'm trying to detect the significant wrapping for each cycle. this also leads to some dropped impulses - but it also adds some ...

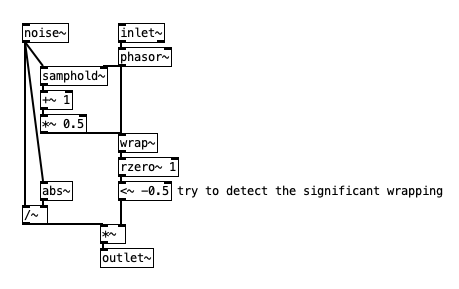
patch: velvet~.pd

... since it's based on the same logic of the randomly offset phasor crossing 1, it also sometimes misses impulses, yes (checked with ~3000Hz):

that's gotta be really rare and only if the random chosen number is stupidly low... basically zero!

@porres said:

that's gotta be really rare and only if the random chosen number is stupidly low... basically zero!

... not that rare depending on the phasor frequency and sample rate. for example: with a 3kHz phasor at 48kHz sample rate, the value of the phasor will increase by 0.0625 per sample (3000 / 48000). so in this case, for ~6% of the cycles, the value won't cross 1 (if the offset is below these 0.0625), since the phasor will already wrap when > 0.9375.

not sure if this is a good explanation and completely valid - i'll wait for others to confirm or correct me.

hmm, yeah, I hadn't checked the values, well, I'm now thinking it makes better sense to set the above value randomly

@manuels said:

By multiplying the frequency with 1/SR you get the phase increment of the phasor. Since there is exactly one sample in each cycle where the sum of the current phase and the increment gets bigger (or equal to) 1, you get the impulse. Now all you have to do is to randomize the phase to get the impulse at a random position.

Just realised, that I didn't consider one important thing here: If the period isn't an integer number of samples, then the method of adding a random number and wrap doesn't work anymore!

yeah, it can't get simpler than this, I guess it can be more sophisticated, to never miss a period, but I also think this is a job for a C code.

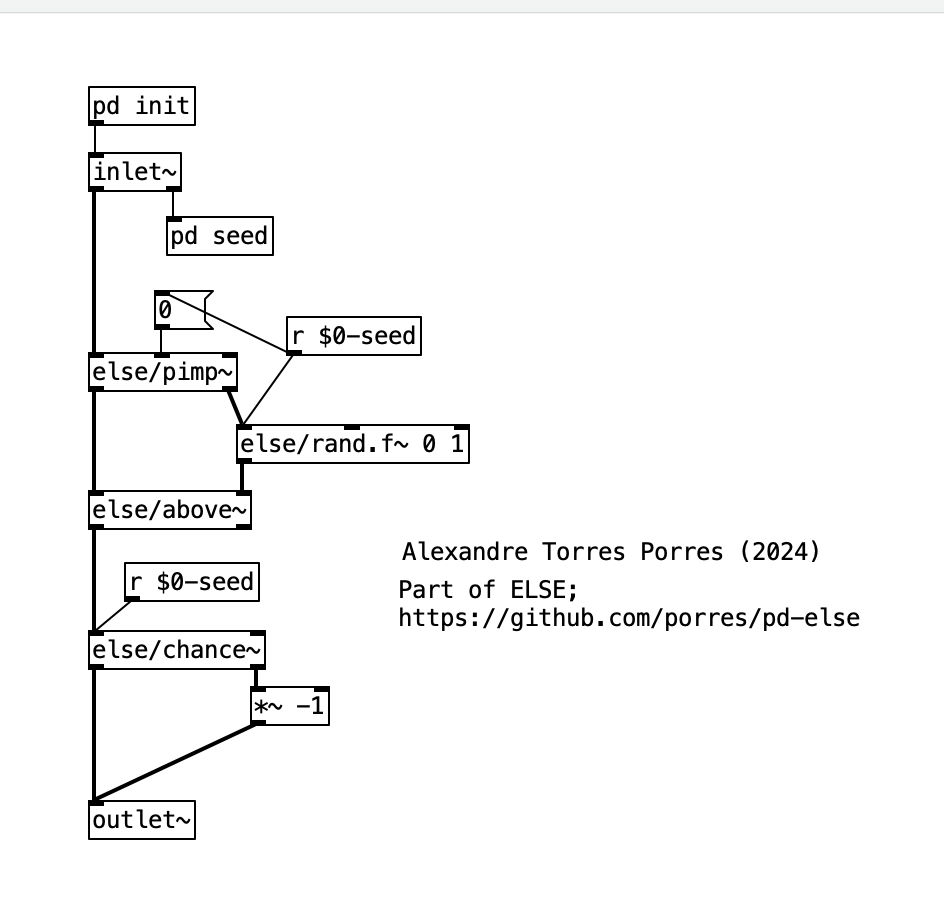
I need to make [pimp~] multichannel, then I will also adapt it to become [velvet~} and it'll also be multichannel, meaning it can receive a multichannel signal to set different frequencies and it'll output a multichannel signal with independent impulse generators.

[else/dust~] and [else/dust2~] are already multichannel, so [velvet~] must also be to follow suit

I'm releasing ELSE RC12 soon, this will hopefully be part of the next RC13 update

@porres said:

to never miss a period, but I also think this is a job for a C code.

To atone for my earlier SC jibe, here's a delay-based approach. (Also, indeed you're right -- I hadn't read the thread carefully enough. Dust / Dust2 don't implement exactly "one pulse per regular time interval, randomly placed within each interval.")

velvet-noise-2.pd

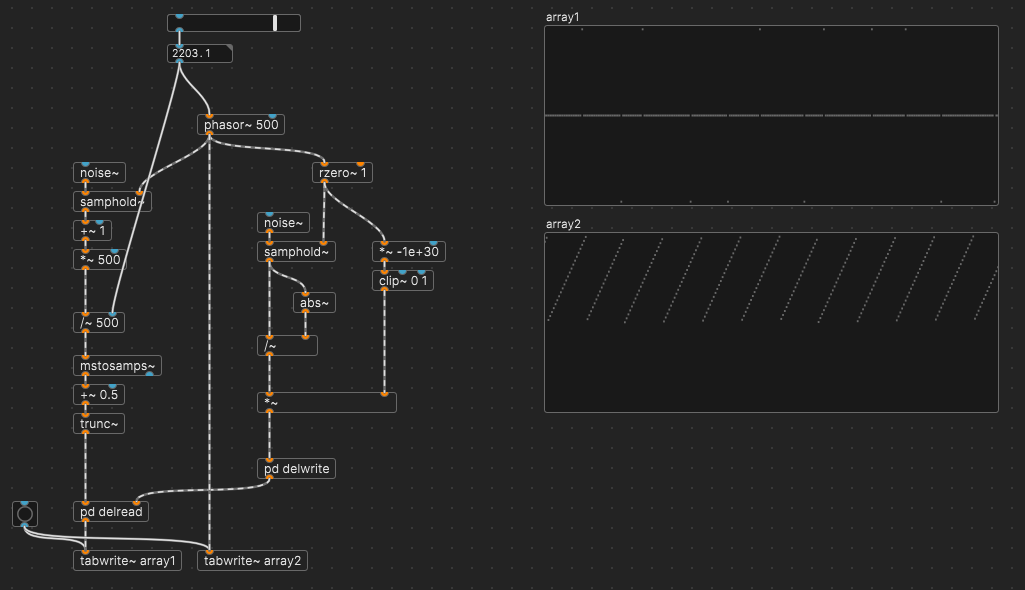
Uses else's del~ because delread~ requires a message-based delay time, which can't update fast enough, and delread4~ interpolates, which smears the impulses. With del~, I could at least round the delay time to an integer number of samples, and AFAICS it then doesn't interpolate.

It looks to me in the graphs like there is exactly one nonzero sample per phasor~ cycle.

hjh

PS FWIW -- one nice convenience in SC is that non-interpolating DelayN doesn't require the delay time to be rounded

(
a = { |density = 2500|
    // var pulse = Impulse.ar(density);
    // for similarity to Pd graphs, I'll phasor it
    // but the Impulse is sufficient for the subsequent logic
    var phasor = LFSaw.ar(density);
    var pulse = HPZ1.ar(phasor) < 0;
    var delayTime = TRand.ar(0, density.reciprocal - SampleDur.ir, pulse);
    var rand = TRand.ar(-1, 1, pulse).sign;
    [DelayN.ar(rand * pulse, 0.2, delayTime), phasor]
}.plot;
)