@porres Sorry, Im not good at explaining ...
There is nothing special about the shift register in those patches, and you are right: Doing linear interpolation with six points is of course a waste since only two points are used. I guess I did it that way because I wanted to switch between different interpolation/smoothing functions in order to compare the results. Only in the case of the Gaussian kernel the precalculation might actually make sense. Maybe not even then.

@porres said:

I didn;t know about "LFDNoise3", is it a new one?

It's been there for years, I'd guess at least 10 years though I didn't check the commit history to confirm that.

Wow, I can't believe they have so many
I see this one is dynamic....

(Deleted snarky and irrelevant comment about the quality of the documentation, which still is better than Max/MSP's help in many respects. But there I go, being snarky and irrelevant.)

The original LFNoise UGens behave like envelopes, where the time to the next control point gets sampled-and-held. So if the frequency happens to be 0.01, the next control point will happen 100 seconds later, no matter how the frequency modulates.

Wow, that's bad

The existence of LFDNoise UGens tells you that SC developers agree with you, and solved the problem (a long time ago). So there's really not much point to taking potshots at this particular target.

and for someone not that much into math, this is not enough, can anyone help? What kind of interpolation is spline? I don't wanna look into their source code

You're into math enough to maintain a DSP-and-other-stuff library for Pd anyway a little dive into the source code shows that SC's plugin_interface headers define a function cubicinterp() that uses the same formula mentioned in the other thread, that's used in tabread4c~.

hjh

@ddw_music said:

You're into math enough to maintain a DSP-and-other-stuff library for Pd

Though not enough to understand or know what "quadratically interpolated" or "cubic interpolated" is supposed to mean so I ask

And again, what is bad about [tabread4~]'s method ("lagrange" so it seems)? And what is good about [tabread4c~]?

@manuels said:

Sorry, Im not good at explaining ...

well please help me understand how you are doing interpolation with such graphs, and what are "basis functions" or "kernel" supposed to mean in this context... or please give me some references to check. Your patch just gave me a new dimension to look at interpolation and I wanna get it

@porres said:

Though not enough to understand or know what "quadratically interpolated" or "cubic interpolated" is supposed to mean so I ask

Sure, "cubic" doesn't specify which cubic (and it would be better if the help did state the formula).

And again, what is bad about [tabread4~]'s method ("lagrange" so it seems)? And what is good about [tabread4c~]?

tabread4~ can output kinks at control points (when the phasor wraps around), where a "kink" is a place where the slope of the output curve changes suddenly. The other formula (labeled Hermite in the SC sources) has a smooth, continuous derivative throughout.

hjh

by the way, cyclone/wave~ has a good detailed documentation that Matt Barber wrote. He also reversed engineered the MAX object. I never fully/really understood any of it. It does mention about "hermite" and says which one is used by SuperCollider. I use the one that is supposed to be in SC for my externals by default. Anyway, I guess I need to dive into this math and theory and I'd appreciatte if anyone could help me with sources

thanks

About those kinks --

tabread-interp.pd

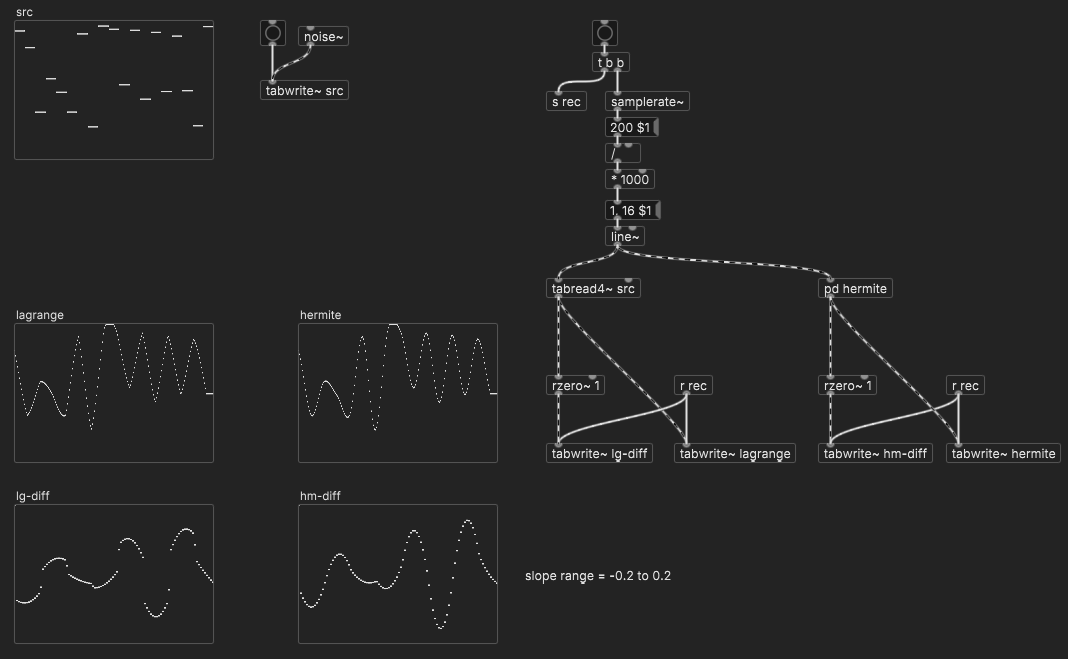
lg-diff -- the slope of the Lagrange interpolation -- shows some gaps; at those places, the Lagrange interpolation will change direction suddenly. hm-diff may change direction at a sharp corner, but those corners link up. The fast oscillation toward the end of this one looks smoother to my eye in the Hermite version, where tabread4~ on the left looks uncomfortably close to straight line segments.

hjh

@ddw_music said:

lg-diff -- the slope of the Lagrange interpolation -- shows some gaps; at those places, the Lagrange interpolation will change direction suddenly. hm-diff may change direction at a sharp corner, but those corners link up. The fast oscillation toward the end of this one looks smoother to my eye in the Hermite version, where tabread4~ on the left looks uncomfortably close to straight line segments.

What is this "hermite" one?

First things first, we need to have proper names for things.

Can anybody really clarify about the terminology of things here?

Like I said, I don't know math I've been asking AI but I don't trust

Let's break things down. First of all, it seems "lagrange" is not the right name to call Pd's interpolator. So I'll stop calling it that. It is cubic of course, and by cubic it means it has a xˆ3 term... it's also the same interpolator used in CSound, according to Matt Barber on the Pd list.

It's bad for some reasons you all seem to know well, and Cyrille made a new one, and it is the same one used by SuperCollider, and it's also the same one I use by default on my ELSE externals.

Now, according to the help file of cyclone/wave~, written by Matt, Pd is supposedly not "hermite", but then, Claude was calling it a 'hermite' one... again, I dunno, let's just call it Pd's. BTW, Cyclone's [wave~] was not supposed to have Pd's interpolator, but we thought "why not?", and added it...

The other interpolators in wave~'s help file are all "hermite", and the one used by SuperCollider/ELSE/tabosc4c~ is "Catmull-Rom Spline". So, "Catmull-Rom" should be specific enough

I still haven't checked the code for the cubic interpolator in SC, but I'm trusting Matt here... and it seems this is the one used in LFDNoise3... and LFNoise2 is quadratic, not cubic, and who the hell knows which one is the quadratic but I'm guessing then LFDNoise3 uses "Catmull-Rom"!

@manuels
in your patch you have quadratic/cubic/quartic B-spline interpolators. You seem to know about this can you elaborate on which interpolators you're using?

cheers

@porres said:

The other interpolators in wave~'s help file are all "hermite", and the one used by SuperCollider/ELSE/tabosc4c~ is "Catmull-Rom Spline". So, "Catmull-Rom" should be specific enough

SC source tree/include/plugin_interface/SC_SndBuf.h:

inline float cubicinterp(float x, float y0, float y1, float y2, float y3) {
    // 4-point, 3rd-order Hermite (x-form)
    float c0 = y1;
    float c1 = 0.5f * (y2 - y0);
    float c2 = y0 - 2.5f * y1 + 2.f * y2 - 0.5f * y3;
    float c3 = 0.5f * (y3 - y0) + 1.5f * (y1 - y2);

    return ((c3 * x + c2) * x + c1) * x + c0;
}

Maybe JMc was wrong to call it "3rd-order Hermite (x-form)" but... he didn't develop this standard formula by himself, so I assume that (30 years ago for SC1 or SC2) he got it from some source that called it this.

I don't have any more time to look at this (project must be completed by next Tuesday) so... I have an lfdnoise3~ abstraction that will work for my use case, hence, I'm bowing out of this chat.

hjh

@ddw_music said:

Maybe JMc was wrong to call it "3rd-order Hermite (x-form)"

No, like Matt says in wave~'s help, and like I mentioned here, Catmull-Rom is a type of Hermite interpolator, so there's no theoretical conflict here.

I don't have any more time to look at this (project must be completed by next Tuesday

Good luck. Anyway, my new rampnoise~ interpolation is the same as SC's cubic one and it should be called a Catmull-Rom for a proper specific documentation. I'm just trying to get things straight.

@manuels
I see now your stuff is something else, they are cubic polynomials for approximation, like bezier curves, is that it? So not proper cubic interpolators, huh?

@porres said:

Good luck.

BTW else/receiver just saved my bacon -- thanks for that!

hjh

glad to hear, even though I'm vegan

@porres said:

@manuels said:

Sorry, Im not good at explaining ...

well please help me understand how you are doing interpolation with such graphs, and what are "basis functions" or "kernel" supposed to mean in this context... or please give me some references to check. Your patch just gave me a new dimension to look at interpolation and I wanna get it

Maybe this is the missing piece of the puzzle? ... Interpolation is just a special type of convolution

The term "basis functions" (that I probably used incorrectly) doesn't matter, and by kernel I was just refering to the function (whether piecewise polynomial or continuous) the input signal is convolved with.

The difference between my examples and some of the others you correctly spotted is also mentioned in the linked resource in the section "Smoothed quadratic". One advantage of a (non-interpolating) smoothing function is that no overshoot is produced. But of course, if you need actual interpolation you have to use different functions.

Another related topic is resampling. This thread may also be helpful: Digital Audio Demystified