Is there a way to expand the range of numbers? Here is an example patch that shows a version of the problem. It is just one example of the issue. Is there no easy workaround?
-
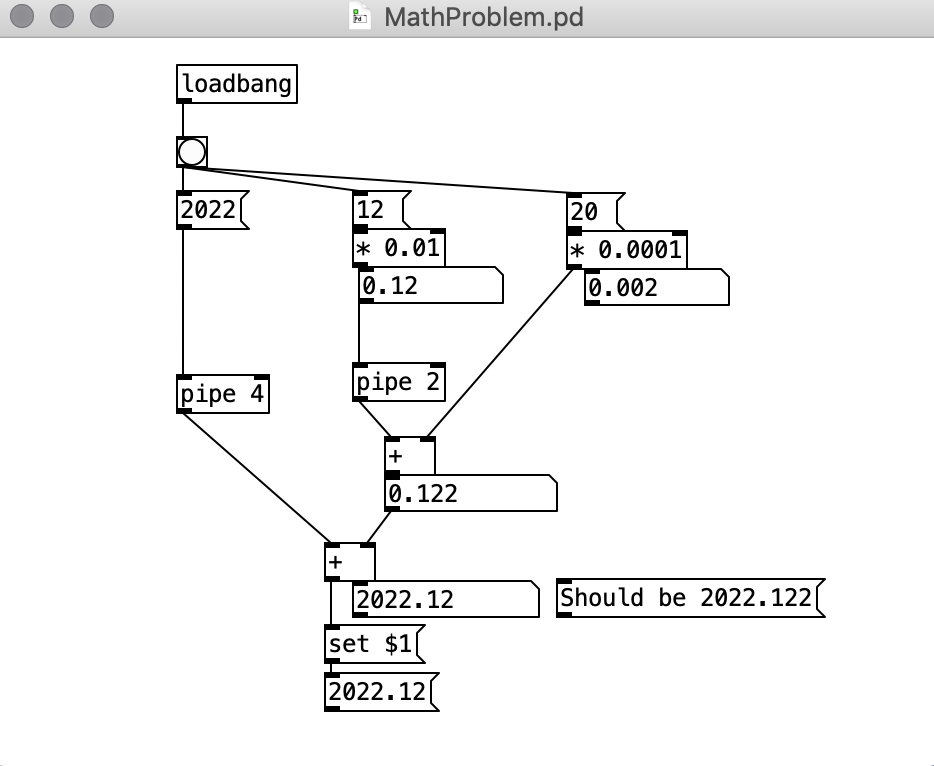
Math detail problem of numbers larger than six or so decimals
-
I am not getting that result though.
Look at the message box at the bottom. I wrote the example too quickly.MathProblem.pd
-
-
@raynovich This is the weirdness I remember:
Untitled-1.pd
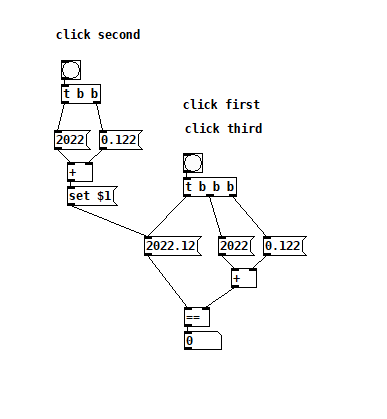
If you save it after it tests equal, the next time you run it it will be unequal again -
And so there is no way to expand the number of digits a number can have? Seems counter to an application that uses numbers in composition. I can imagine there are some workarounds, but I wish there was a way to expand the numbers allowed to assess.
It seems that the == object cannot assess a number with seven digits.
-
@raynovich I agree with your larger point. I don't understand why there isn't more interest in double precision floats. Single precision floating point only gives you so many digits--I think just one or two digits past where Pd is truncating. You can get control of those digits using ugly tricks like this:

The backslash-escaped space before the pi digits stops Pd from truncating it. -
@raynovich if you just want to display the number to more than 6 digits then you could use
[makefilename %.7g]to display to 7 total decimal places (use a symbol box instead of a float box to display)if you want to store/generate the number you can also use
[float 24]from iemlibof course you might see some of the 32-bit representation come into play...
edit: better format specifier
-
A numeric representation with a finite number of digits is always an approximation, unless it's a rational number and the prime factors of the denominator are all prime factors of the base.
2022.122 can be represented accurately in decimal because the denominator is 1000, with prime factors 2 and 5 (same as base 10).
1/3 cannot be represented accurately in decimal because base 10 does not include 3 as a prime factor.
In binary floating point, base 2 has only one prime factor, so the only numbers that can be represented accurately are those whose denominator is a power of 2. 0.25 = 1/4, ok. 0.2 = 1/5, not ok.
Many people get confused because they wrote an exact decimal value and assume that it will be exact in binary. It may very well not be. 2022.122 is one of those (the denominator has three factors of 5, which binary cannot handle).
One takeaway is that == tests are often invalid for floating point. You shouldn't expect it to work, actually. It isn't weird. It's in the nature of the number system.
Similarly, there's no "right pi" and "wrong pi." Every representation of pi in a computer is wrong. The expr example merely generates a wrong pi whose wrongness matches the later operations.
Double precision pushes these issues further away so they are less visible -- but 2022.122 is a repeating binary in double just as much as in single precision. It would be good for Pd to move up to doubles for control messages though.
hjh
-
hjh, I get it. The thing is that I am trying to just write the "number" for a date. . . . so, it feels rather wrong, but I get it. Without double precision, a "number" can only be indicated to six digits. . . I do not know the exact number but I get the idea.
I was trying to write a date as a number. . . . yes, I can do it other ways, but this was a "simple" way I was hoping to do it. It is cool that I cannot, but there is another piece I want to write that requires even more detail than double precision. The other thing is that I cannot even write the number as a symbol which seems even more annoying.
Anyway, I am good with it all. Just wish we could have more precision.
-
@jameslo said:
@whale-av But they're only there temporarily. Once you save and reload the value, it's takes on the truncated value. That's why I compute pi every time I load a patch that needs pi. There's also the limitations of single precision floats,
it would not make much sense to display something which is incorrect anyway, the display limit takes into account the precision, well, more or less.
regarding your pi, that probably only makes sense if it happens within an [expr]. however it cant hurt, and do this kind of thing the same way.
2022122 already has a mantissa of 111 0110 1101 0111 0101 0000 (all 23 digits)
the image from james above shows the "issue" very well.


