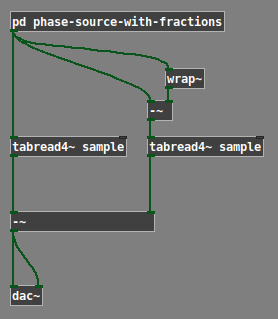
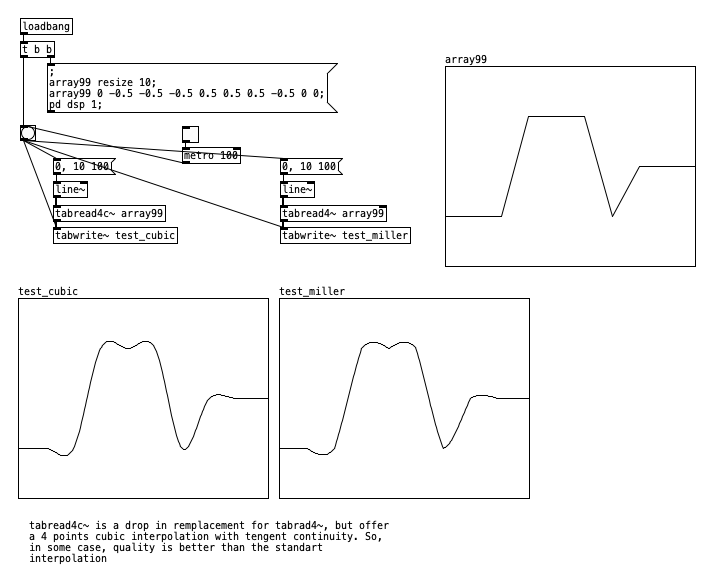
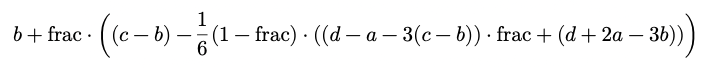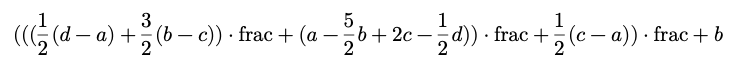Sometimes when you do time-stretchy/pitch-shifty things like in B14.sampler.rockafella.pd, when you return to normal time/pitch you are left indexing in-between samples using tabread4~. That's gotta introduce some fidelity loss, no? Has that bothered you enough to make you write something clever to get the indexing back to integers? If so, please share!
Here's a little test I wrote to see if I could hear the difference: sound quality test.pd . Load whatever sound you think would clearly expose lo-fidelity playback. You can compare integer indexing with fractional indexing and adjust the fraction. I think I hear a difference but I'd have to do a bunch more work before I'd declare I do and I'd rather ask you kind folks first. Plus I think you'll find it fun to try to hear the difference.