Can not quite figure out what I am missing here regarding the operation of pd. Left works exactly as expected, signal cancels and no output; right sort of works if block size is one and you are careful about creation order but you only get maybe 50% cancellation and more distortion than cancellation. I have tried every feedback method I can find and tried to explain the results through my understanding of how pd works and the usual reference sources but I can not quite piece it together or find an answer.

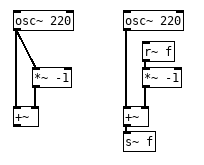
Is there a way to make this work?

@oid It's interesting that s~ and r~ now accommodate block sizes other than 64, it wasn't always the case (https://forum.pdpatchrepo.info/topic/12459/reducing-block-size-to-reduce-delay-of-send-receive). I'm gonna have to unlearn that "fact".

I think you may be applying analog intuition to digital. Here's a little rewrite that makes things a little clearer to me:
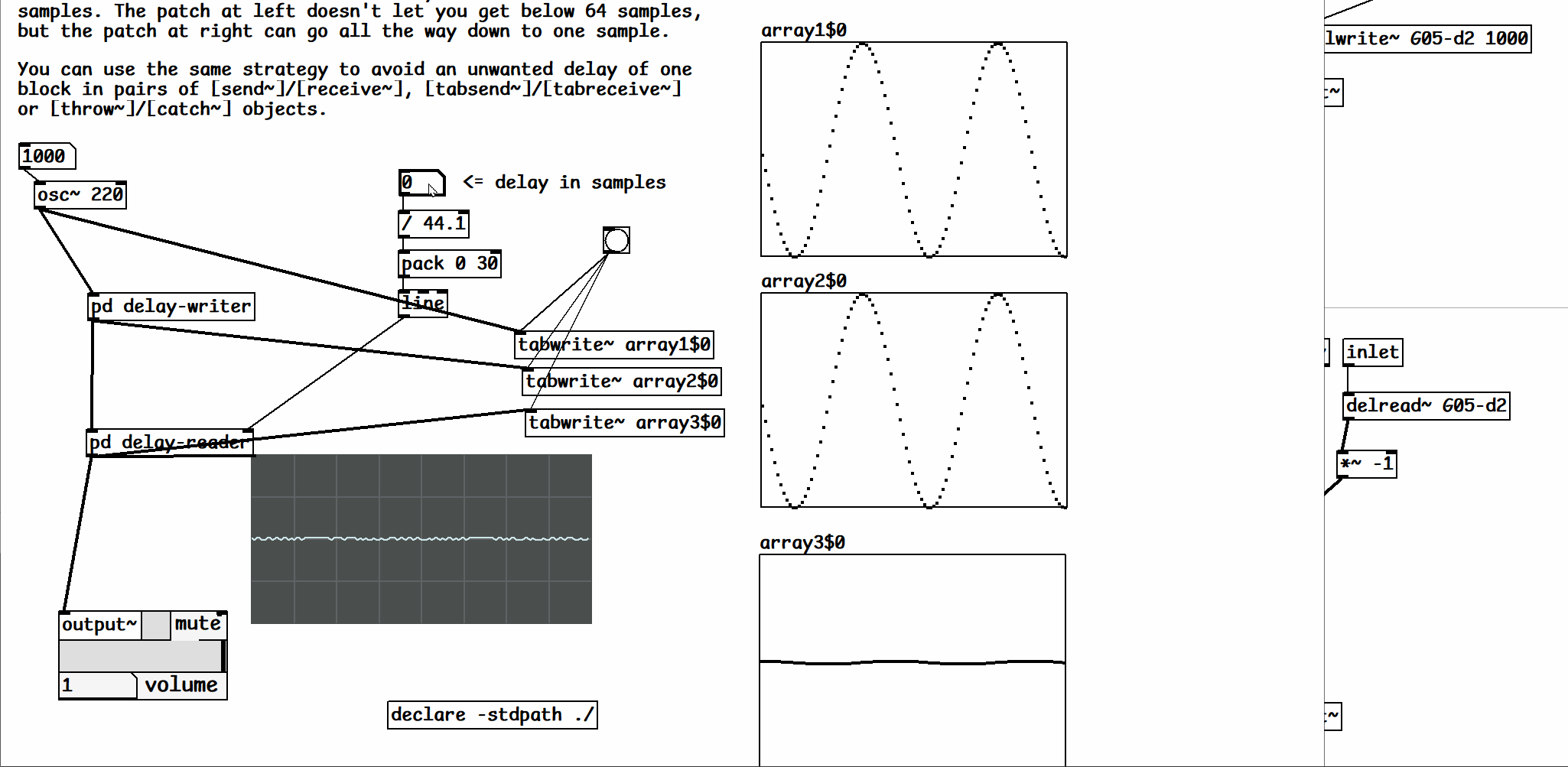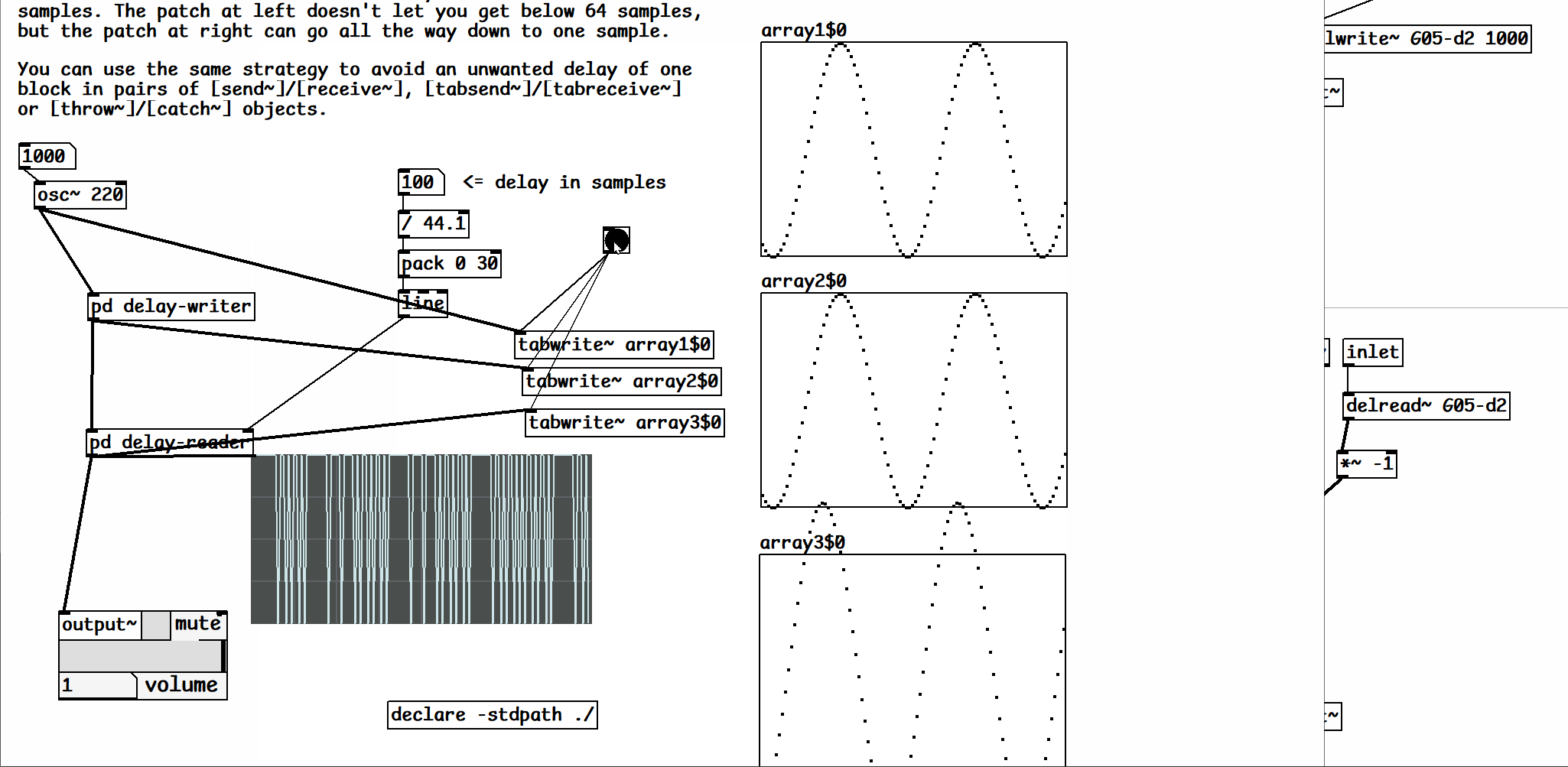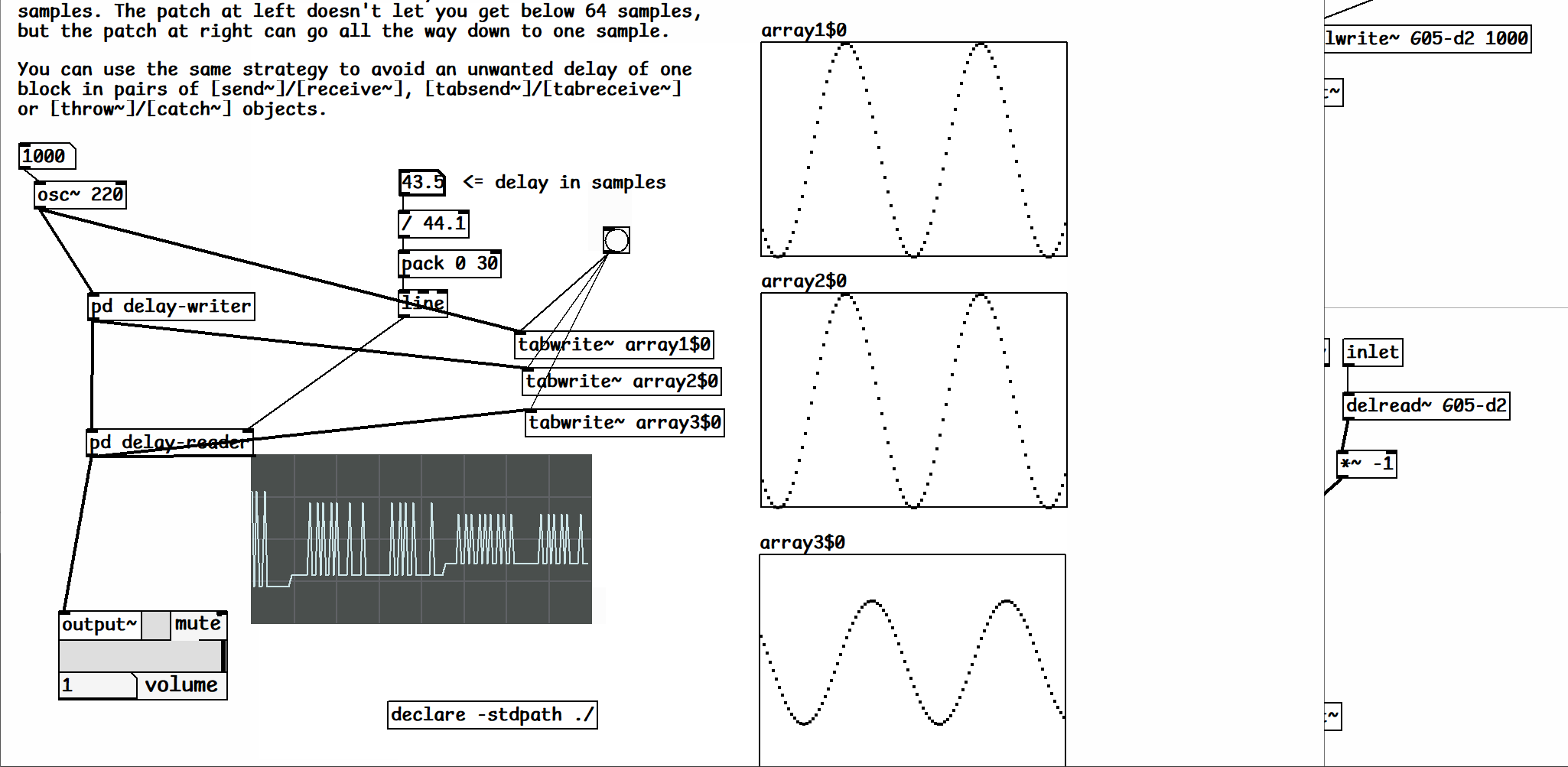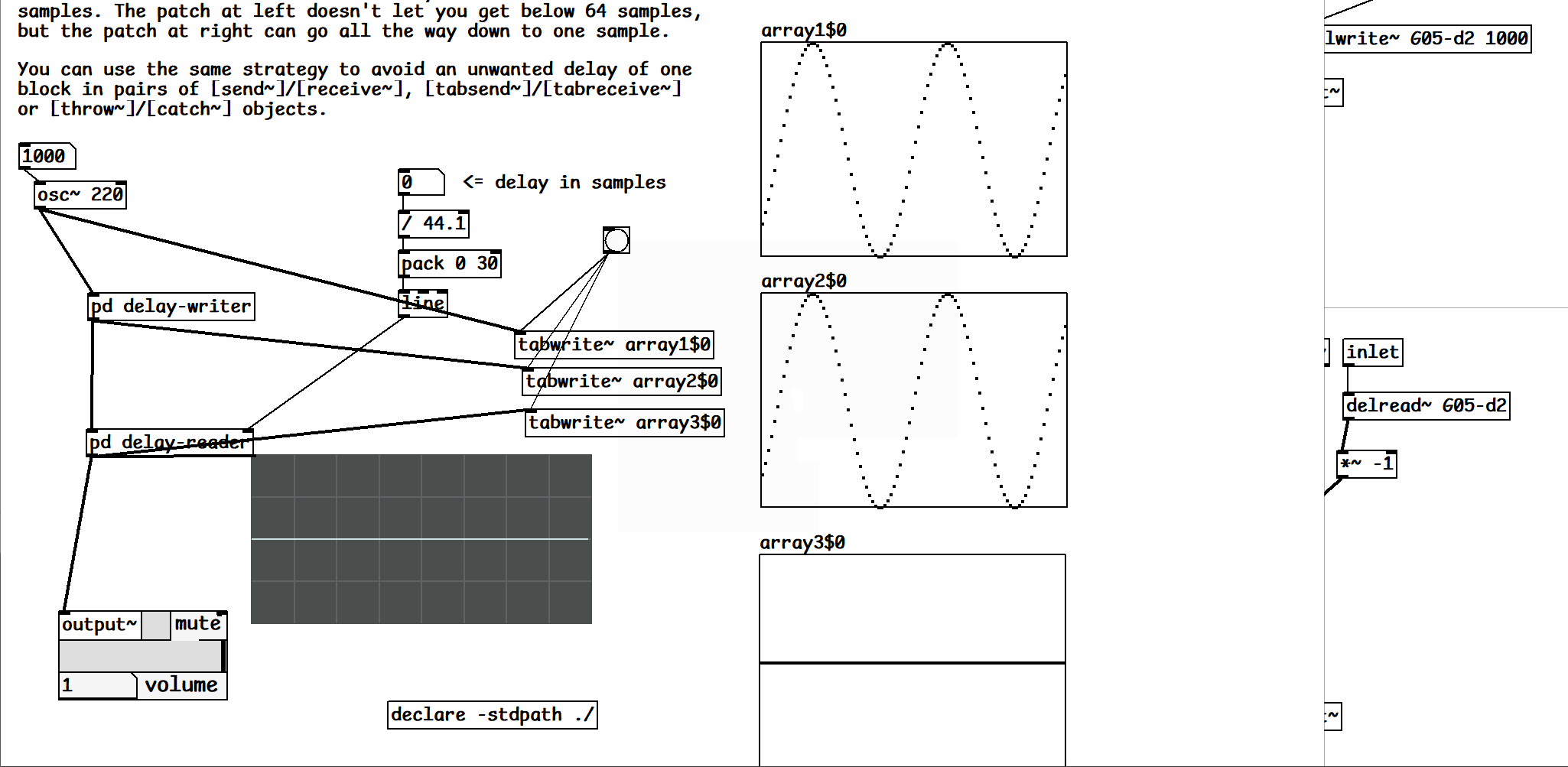
oid fb test 2a.pd

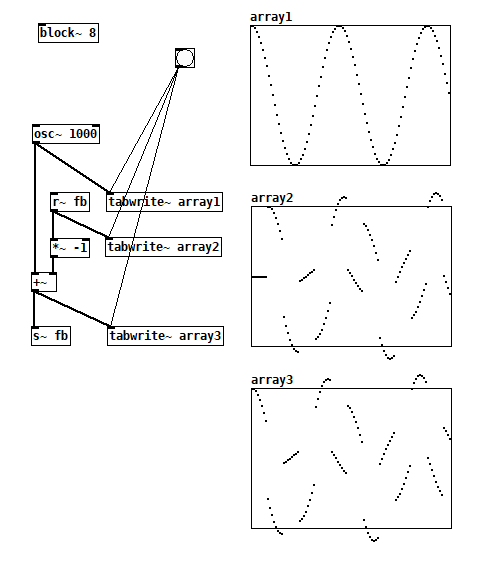
The arrays are showing the very first audio computations because I clicked the bang before turning on DSP. Array3 contains the sum of the osc and the inverted fb and you can see that array2 starts with 8 0 samples due to the latency of the s~/r~ pair. You get the first discontinuity in array 3 because you're asking osc~ to suddenly jump down 1 in array2. And the next discontinuous segment makes sense because you are adding osc~'s mostly negative slope with inverted fb's even more positive slope. And it's close to zero because the former is close to -1 and the latter is close to 1.

Here's another one where I tried to get rid of the discontinuity by starting osc~ at 0. It still has some surprising shapes.

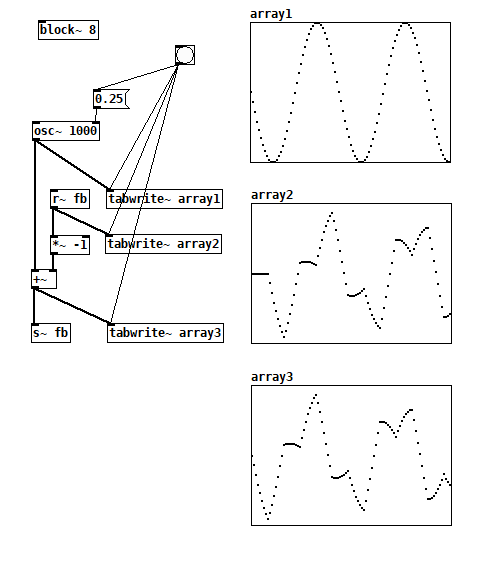
I'd love it if someone who has an analog synth could patch that and see if they get similar results.

@jameslo said:

I think you may be applying analog intuition to digital.

I absolutely am, playing with pd is a little to close to drawing schematics for me and my brain which has been programmed by 25 years of play with analog electronics. Never had this problem with CSound or SuperCollider, working at the text level never taps into the electronics portion of my brain. Still not completely clear on this, mainly why it would not work with a block size of one, I would expect it to mostly cancel, I think my only hope is to go to pen and paper and essentially work it out sample by sample, only way my analog brain will understand. I have been trying to understand this exact quirk on and off for years, my brain just can't deal with it.

I'd love it if someone who has an analog synth could patch that and see if they get similar results.

It would cancel almost completely, in an analog synth there would be some distortion, amplitude differences and phase delay which would cause an insignificant (by analog synth standards) amount of the signal to remain. If it didn't cancel our humble opamp would not exist and the electronics world would be a very different place.

@oid I was coming back to delete that sentence about analog intuition, but you had already quoted it. The reason is that I'm not convinced that an analog synth wouldn't behave similarly. Don't op amps become unstable if there are phase shifts in the feedback loop? And isn't that what frequency compensation is all about? In this case, it's not just phase shifts, but delay.

Also not sure why CSound or SC wouldn't produce the same result as Pd.

@oid phase cancellation due to a signal added to itself delayed by 1 (or more) sample(s) is the building block of most digital filters.
you basically recreated [rpole~ -1]
(and if you subtract the 1-sample delayed input instead of the output it's [rzero~ 1])

One way to think about it is that a signal with a delay added to itself is a comb filter, and if the delay is 1 sample then there will just be 1 comb 'tooth' in the amplitude response
(so you can analyze the frequency response of comb filters for other sample lengths of delay)
https://ccrma.stanford.edu/~jos/pasp/Comb_Filters.html
allpass filters (used to build phasers) are very related
https://ccrma.stanford.edu/~jos/pasp/Allpass_Two_Combs.html

this isn't so much a 'pd' thing, more of a 'digital/sampled audio' thing

@seb-harmonik.ar But it's the negative feedback coefficient that's throwing me. I'm used to it being a positive fraction < 1. Does the comb filter theory cover negative coefficients? The equations look as though they do, but whenever I see diagrams, they always show positive coefficients.

Edit: I just returned to a flanger I wrote and flipped the sign of the feedback. It didn't sound crazy at short delays and the pitch of the primary comb peak dropped approx an octave.

@jameslo of course, 'comb filter theory'' is just math and that can account for negative coefficients (and even imaginary/complex ones :->)
if you use a negative coefficient then it will be an octave down from where it would be if positive, because the original period cancels exactly, but at an octave down it is constructive.
the wikipedia article seems like it might have some insight about negative coefficients (essentially the 'teeth' are shifted by an octave down)
so it is an octave down, but only contains odd harmonics of that fundamental (the negative part will catch the 2nd half of a sine period in the middle of the 'transition', and constructively interfere with the 1st half of the 1st period if the harmonic is odd but if even it will be destructive)
https://en.wikipedia.org/wiki/Comb_filter

when we take the delay down to 1 sample I believe you get a highpass instead of a lowpass, because now an 'octave down' from the samplerate (or 0) is nyquist

@jameslo said:

Don't op amps become unstable if there are phase shifts in the feedback loop?

Sometimes. Way up high above the audio range an opamp's phase reverses and if your feedback network also reverses the phase of those frequencies your negative feedback becomes positive feedback and you amplifier turns into a 10mhz oscillator.

And isn't that what frequency compensation is all about?

Frequency compensation drags the frequency response of the opamp down below the point where the phase reversal happens so it can never be reached. We can play around with phase in the feedback loop all we want to as long as we are mindful of what is happening up where the phase reverses, you can either cut that range out of the equation with frequency compensation or design around it.

Also not sure why CSound or SC wouldn't produce the same result as Pd.

As I said, it is me and not them. The pd interface being so much like a schematic editor causes me to fall into analog habits. I assume Csound and SuperCollider would have the same issues but I never find myself trying to do this stuff in them.

@seb-harmonik.ar said:

phase cancellation due to a signal added to itself delayed by 1 (or more) sample(s) is the building block of most digital filters.

I have known this for a good long while but I am just starting to understand it, lots of stupid assumptions to discover and unlearn. Thanks for the reading, that filter book is going to keep me busy for awhile.

@oid

I get a dsp loop from that

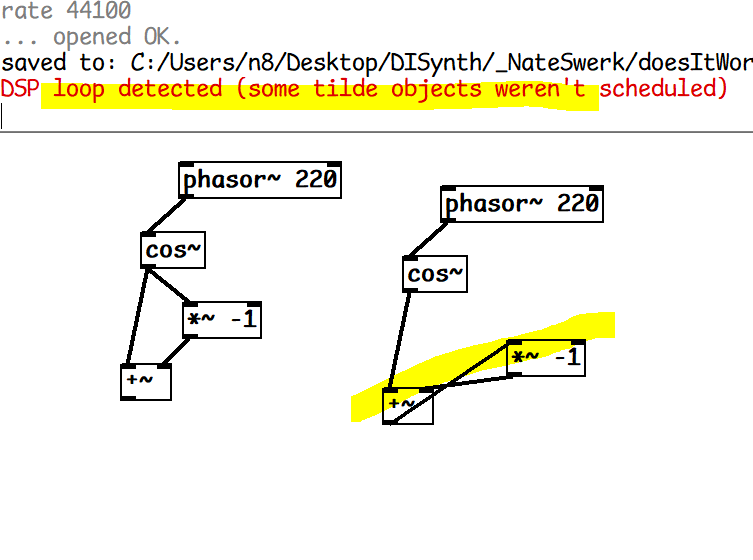
there's no parallel concurency in digital audio programming - there's always an order of execution, Im thinking with correct blocking it should work, delay the feedback and the osc~ but from experience when pure data has trouble being perfectly exact at something its easier to go dig around for an external, people usually write them to make up for certain thing vanilla doesn't do easily

I played around with the help browser (the audio section is also miller's book) - using the Order of Feedback example for a proper flanger I was able to get it down to Almost there - I think its not totally cancelling because of a problem with the tinyiest part of 32 bit floats tho, 32 bit floats are just weird guys

doesItWorkFreedbak.pd

@fishcrystals I'm not at my computer but I think it might be due to the necessary 1-sample guard point for cubic interpolation. You might have more luck with regular [tabread~]

@fishcrystals Interesting, I tried the subpatch trick but I got a DSP loop error but I did not put the [*~ } and [+~ ] in the subpatch so that may have something to do with it. My reasons for exploring this would not really be solved by an external, mainly trying to figure out the audio side of pd a bit better and vanilla is the best way to do that. Thanks.

@jameslo I was probably a bit cavalier regarding my comments on this working on a modular, I should have said it would work on any well designed modular system. Not all modules respect phase, a simple amp and inverter on a modular can actually be quite complex circuits which depending on their design may or may not play well with feedback, the feedback you apply would be in addition to any feedback they have and mixing modules from different makers is an unknown in many ways. But I suspect it would work much of the time. I was cavalier regarding being able to do anything you want with phase in the feedback loop of an opamp, there are limits but a good number of filters and oscillator circuits are opamps with feedback loops that play with phase, like phase shift oscillators. I responded right before I was to head out the door and did not take the proper time in that response.

@oid yeah, definetly worth it to work out how PD thinks. Im not sure about other ways but it looks like blocking a delay line in subpatches works to sync feedback

thanks for the tip @seb-harmonik.ar once I plopped in [delread~] instead of [delread4~] its working great - interesting how it looks like it tries to repeat phase cancellation when the samples of delay / 44.1 = the oscillators frequency or another ratio with the sample rate

doesItWorkFreedbak.pd

@fishcrystals I don't understand, where's the feedback? [delay-writer] is just feeding signal forward to [delay-reader], directly and through the delay line, no?