In Pd of course, anyone?

I think the above algorithm could be done as a patch in Vanilla, but you have to go in a lower level than using [phasor~].

I endorse all the struggle in implementing this as a Vanilla patch, but we gotta realize that sometimes life is short and how Pd is not actually well suited to implement DSP algorithms, specially Vanilla.

I have many low level objects in ELSE that make life so much easier, and even so, sometimes you gotta go into C

improved a bit, now it does have negative impulses, and made some more intense tests, it all works well and up to the nyquist frequency, where it becomes a "clip noise" (same as [else/white~ -clip]).

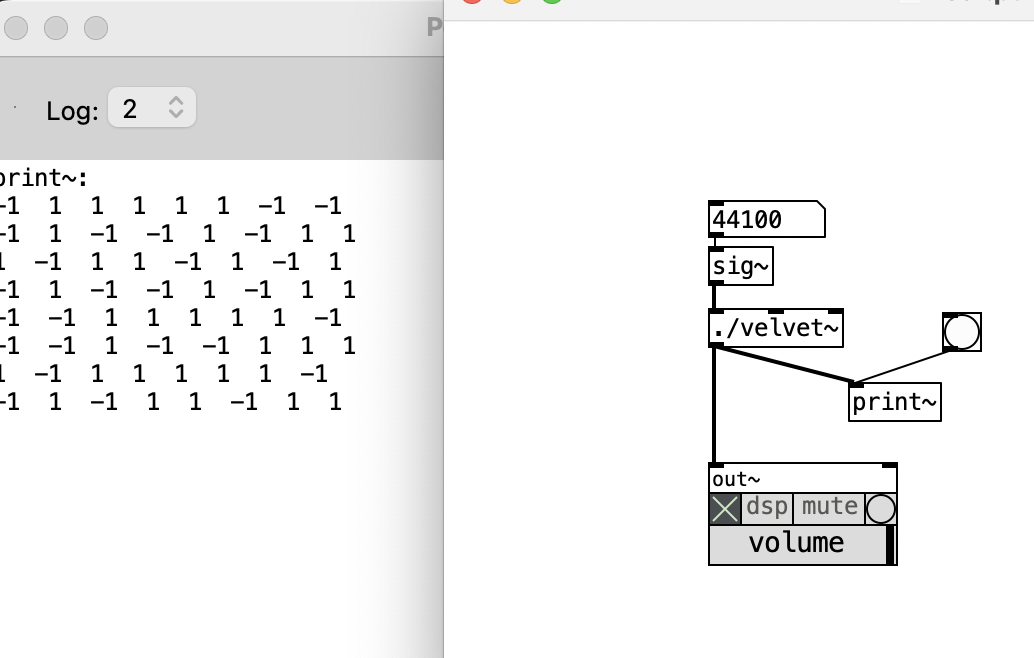
@ben.wes EDIT: this brings up an important question though (which is also probably answered in the papers): are consecutive values of 1, 1, 1, -1, -1, -1 or -1, 1 allowed? not sure ... but these wouldn't be actual impulses anymore then, right?

Yes, it is answered in the paper.

@porres No, they are not allowed, according to the paper @ben.wes linked to..... https://acris.aalto.fi/ws/portalfiles/portal/13412521/applsci_07_00483_v2.pdf

The note to the screenshot he posted states.......
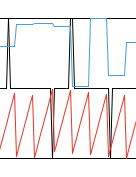
"Figure 1a shows the first 500 samples of an example velvet-noise sequence with these parameters.
There is only one non-zero sample seen between any two grid boundaries."
The graph has an average pulse distance (interval) of 20 samples (the chosen parameter).

So all the space between impulses in the chosen interval must be zero.

For a Pd block size of 64 (if that is chosen as the interval size) there should be just one impulse per block.

Yes.... [phasor~] is a disaster zone.... why I went for [vline~] even though that needed a control rate input.
A single impulse per interval should be easy now you have done the hard work in C.
Maybe you could add the interval size to your [./velvet~] external as a creation argument?
My patch [velvety-2] puts a lot of -0 values which looks very messy, but with an interval of 64 samples [print~] should produce just one non-zero sample per block....

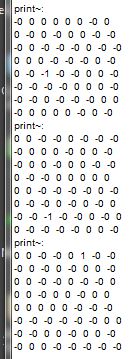
For an interval of 2 samples the output should be as per my [velvety] above.....
.... but it is not useful as there can be no time variation within the interval....

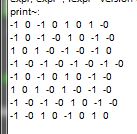
.... and of course an interval of 1 sample is impossible.... as in your current external...... because they cannot be impulses without being followed by a zero.
Your print~ above is a time modulated square wave.

Great work though.
I am jealous of those of you that have learnt to program in C.
David.

well, what if the frequency is equal to the sample rate? then it's gotta be a bunch of 1/-1 ("clip noise")

I'm actually having issues above nyquist, and I guess the idea of velvet noise is not to be used for such high frequencies anyway! Nonetheless, I want my object to be able to go without issues up to the sample rate frequency and I guess the best strategy is just to use a different logic above nyquist as my code is actually flawed for such high frequencies...

Your print~ above is a time modulated square wave.

no, that is a clipped white noise, as I mentioned. It's what you get with [white~ -clip]. Or SC's ClipNoise... I just want to be able to go up to the sample rate so you can achieve full whiteness with this object. In my [pink~] and [brown~] noise objects I can also control the "whiteness" by the way

they are not allowed, according to the paper

that is just what it is for about 2Khz frequency input, which seems like a reasonable rate for velvet noise... I just want to be able to go up to 20khz, 30khz, 40khz and up to the sample rate... whatever it is (44.1 khz being the usual one)!

Maybe a true velvet noise shouldn't reach nyquist and if it did then you'd have just interleaved zeros... I guess I can do that and change the way things work for the above rates, as I doubt there is any perceptual difference if I could change the impulse positions randomly in this case...

For the Nyquist, my idea is that for the 2 sample period the impulse has a 50% change of coming in the first or second sample... so whenever I have the possibility of at least a 2 sample period I wanted to be able to randomly choose it... but my code is not working well for that.

I'm trying to find a better and more sophisticated idea for the algorithm. We need to find the number of samples in a period and then randomly choose where to place it. The problem is that if we do this explicitly this way, it doesn't seem to work well for a dynamically changing frequency input at audio rate... trying to find a way here...

@porres said:

I'm trying to find a better and more sophisticated idea for the algorithm. We need to find the number of samples in a period and then randomly choose where to place it.

I'm not in C, but I think I kind of did exactly that in my latest version, trying to solve the problem with non-integer periods. Here it is (commented in the patch) ...

velvet-noise.pd

Could certainly be optimized in some ways (especially using ELSE objects). But does it even work? I don't have a good method to test it, unfortunately.

@manuels said:

Could certainly be optimized in some ways (especially using ELSE objects). But does it even work? I don't have a good method to test it, unfortunately.

nice! - i like this counter for samples per phase:

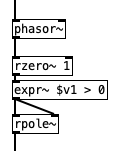
... from what i tested: it behaves perfectly well up to nyquist - although also in this range, there are sometimes consecutive non-zero samples (which i'm still not 100% sure if valid. see the 1, 1 in the middle below. the blue graph is the scaled offset per phase).

@ben.wes Thanks again for testing, really helpful!

Yes, it's true, that I didn't care about consecutive non-zero samples. For now I'm not sure what's more important: to comply to this constraint or to behave properly above nyquist.

The problems with frequencies above nyquist, that you found, probably have to do with the representation of small floating point numbers. I should have used [expr~ int($v1)] to get real zero values. Can't fix it right now, but I'll try tomorrow ...

@manuels said:

Yes, it's true, that I didn't care about consecutive non-zero samples.

Is there a rule not to have consecutive samples? If so, Nyquist is the limit

Ok, I changed the algorithm a bit and now I think I nailed it and solved it for frequencies up to Nyquist and above! I'm just randomly choosing any sample in the period, from first to last and I don't have if there are consecutive samples, like the last sample from the previous period and first sample from the current one.

    for(int j = 0; j < x->x_nchans; j++){
        for(int i = 0, n = x->x_n; i < n; i++){
            double hz = in1[j*n + i];
            double step = hz * x->x_sr_rec; // phase step
            step = step > 1 ? 1 : step < 0 ? 0 : step; // clip step
            t_float imp = 0;
            t_float r =  x->x_rand[j]; // - step;
            if(phase[j] >= r && ((lastphase[j] < r) || (x->x_1st[j])))
                imp = velvet_random(x) > 0.5 ? 1 : -1;
            out[j*n + i] = imp;
            x->x_1st[j] = 0;
            if(phase[j] >= 1.){
                x->x_1st[j] = 1;
                x->x_rand[j] = velvet_random(x);
                while(phase[j] >= 1.)
                    phase[j] -= 1; // wrap phase
            }
            lastphase[j] = phase[j];
            phase[j] += step;
        }
    }```

ok, just implemented bias and regularity as well... which was really a no brainer, cool! I like how I can turn this into an impulse oscilator if I set the regularity to maximum and bias to a single polarity. Then we can just introduce a little bit of randomness in both cases.

Wow, this is a pretty cool object and random noise generator. Thanks everyone who participated

I will announce when I officially include this object, I might squeeze this one in for the next upcoming release in a week or so

having the object at full sample rate frequency and then adjusting the bias to a low value, just so a few of the samples are of an inverse polarity, also creates a nice texture!

Done!

Now for the big question, where are the Reverb algorithms based on velvet noise?

here's the code, object should be in the next release any time now, just need Tim to help me compile a few things... https://github.com/porres/pd-else/blob/master/Code_source/Compiled/audio/velvet~.c

thanks again

So here's the fixed version: velvet-noise-fixed.pd

It wasn't just the issue with small floating point numbers, but more importantly it now didn't work with integer periods. In this case, of course, the period must never be reduced by one sample!