Hi
So ive been trying to make a very simple, basic fm8 emulation. Doesnt have to be exact at all, but just wanted it close enough so i could reverse engineer some of the patches in pd. I found this site https://www.native-instruments.com/forum/threads/modulation-index.6534/ detailing how the mod index is calculated, but i didnt have much success with this, it didnt sound much like it. Then I found this site detailing how the mod index is calculated for the DX7 http://www.angelfire.com/in2/yala/t2dx-fm.htm and i tried that out. When the mod index is maxed out it sounds way more extreme and than on the FM8. I have the formula right because I can see its the same mod index in the table on the website, is there something else I'm missing? Anyone had any experience emulating the FM8/DX7?
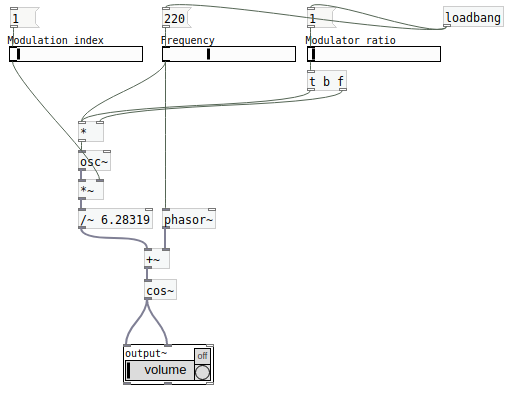
Here's my patch:
fm8 modelv1.pd
Thanks
R


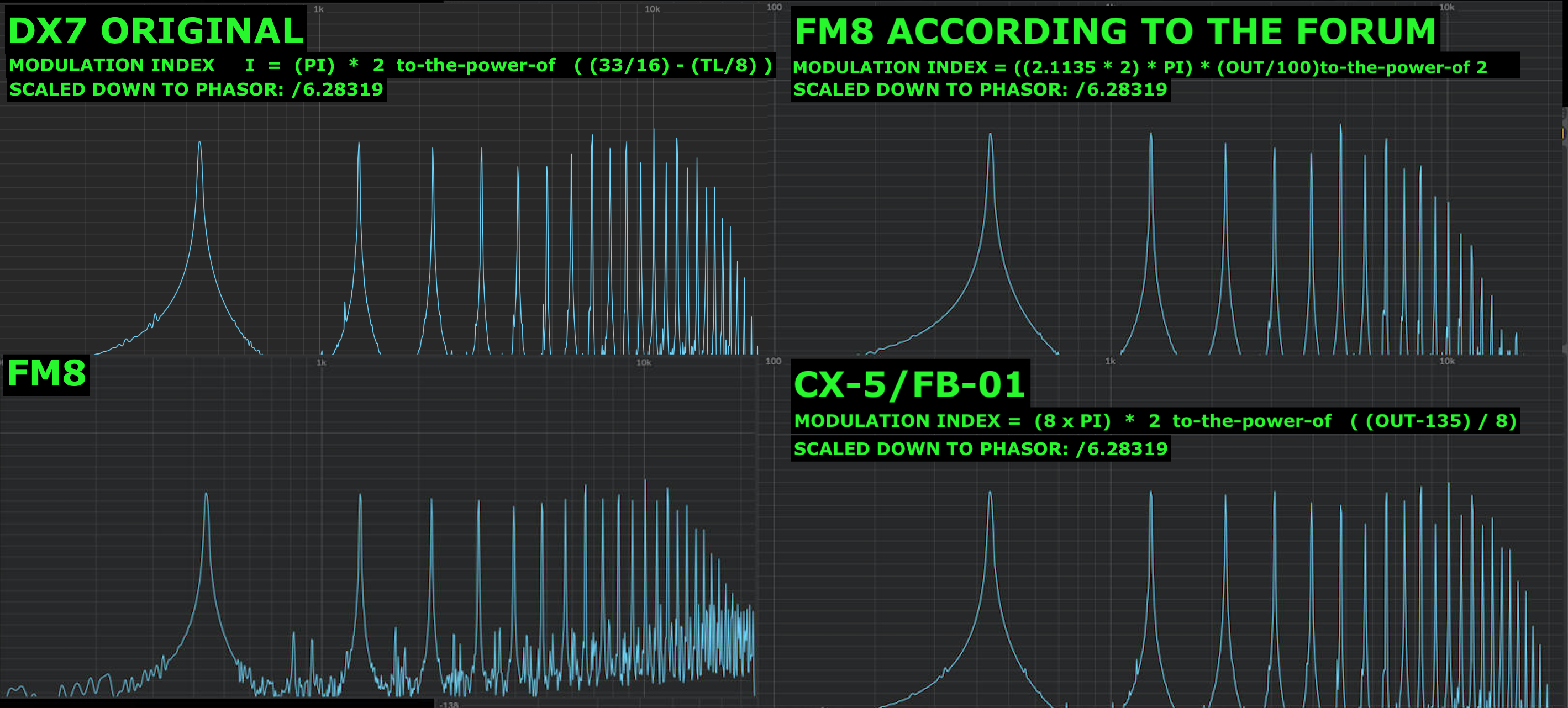
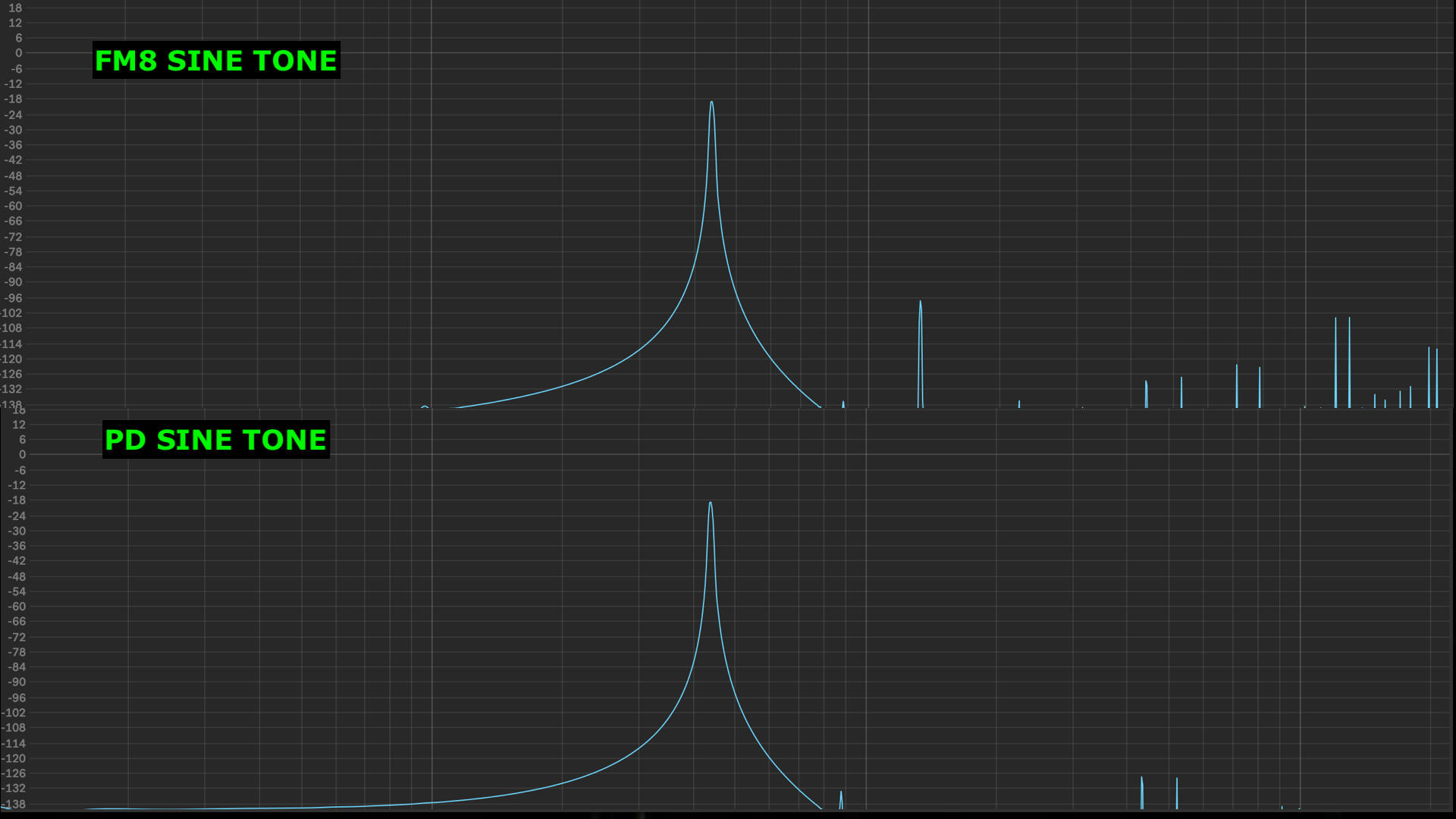
 Glad to help. It just happens that I was working on this less than a month ago for a synthesis theory class.
Glad to help. It just happens that I was working on this less than a month ago for a synthesis theory class.