Hi, I'm stuck in a simple exercise from Loadbang book, which is : "Create a glissando that we hear as linear and one that we hear as logarithmic from C3 to C6." That's my functional linear version:
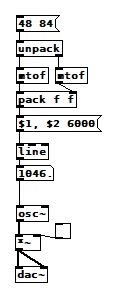
However, about the logarithmic version (and other generalizations I can think about, like exponential, quadratic, etc...), is there an easier way than manually getting the parameters of a function like A*e^x + B and using expr?
-
Logarithmic glissando
-
@Cmaj7 I usually just use
[line~]going into[mtof~] -
@Cmaj7 This should offer some guidance on making variable shaped curves. https://forum.pdpatchrepo.info/topic/12967/control-domain-waveforms
I really should update that abstraction, one of my first serious attempts, a little embarrassing in execution but it does the job. Works by doing the line in the 0 to 1 range and then scaling as needed so you can use [pow] to change the curve as just by tweaking the right inlet value, a power of 0.1 gives a square root curve, a power of 2 gives exponential and you can go higher or lower yet. -
in the logarithmic version you would move the mtof behind the line.
-
Sorry to be a hair-splitter here, but the assignment in the OP clearly says:
"Create a glissando that we hear as linear and one that we hear as logarithmic from C3 to C6."
What we hear as a linear sweep is a log sweep: we perceive the same distance from A3 (220hz) to A4 (440hz) as we do from A4 (440hz) to A5 (880hz), while in reality the latter is twice as long as the former.
Hence, what we will hear as a linear sweep is @seb-harmonik.ar 's solution, while a linear upwards sweep like the one in OP's patch will sound as if it's slowing down exponentially - whether that qualifies as "hearing it as a logarithmic sweep" I will leave to the math geeks to ascertain
-
it depends on what you treat as base. when you think in note numbers and not in hertz, it is the other way round.
but... we would have to distinguish between up and down. mtof wont do that of course.
(in my portamento abstraction the user may choose different settings for up and down individually. including "off"... )
-
however the order will be like that: if you use a whatever scaling algorithm on the line output, the mtof still has to be on the end.

-
One of the very early lessons that I teach in my interactive multimedia class is range mapping, where I derive the formulas and then leave them with ready-to-use patch structures for them.
-
If it's based on incoming data, first normalize (0 to 1, or -1 to +1, range). If you're generating a control signal, generate a normal range (e.g. [phasor~] is already 0 to 1).
-
For both linear and exponential mapping, there's a low value
loand a high valuehi. (Or, if the normalized range is bipolar -1 to +1, a center value instead oflo.) -
The "width" of the range is: linear
hi - lo, exponentialhi / lo. -
Apply the width to the control signal by: linear, multiplying (
(hi - lo) * signal); exponential, raising to the power of the control signal =(hi / lo) ** signal. -
Then (linear) add the lo or center; (exponential) multiply by the lo or center.
One way to remember this is that the exponential formula "promotes" operators to the "next level up":
+-->*,--->/,*--> power-of (and/--> log, but that would only be needed for normalizing arbitrary exponential data from an external source). So if you know the linear formula and the operator-promotion rule, then you have everything.- linear: (width * signal) + lo
- exponential: (width ** signal) * lo
(Then the "super-exponential" that bocanegra was hypothesizing would exponentiate twice:
((width ** signal) ** signal) * lo=(width ** (signal * signal)) * lo.)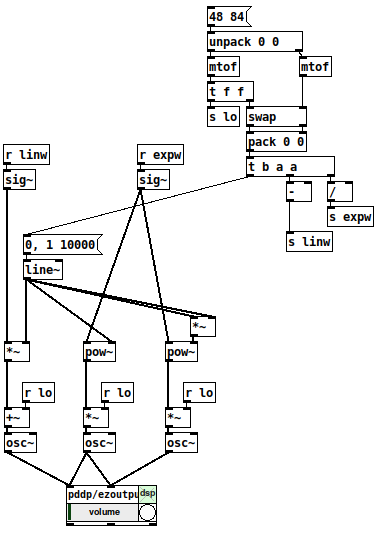
[mtof~] is a great shortcut, of course, but -- I drill this pretty hard with my students because if you understand this, then you can map any values onto any range, not only MIDI note numbers. IMO this is basic vocabulary -- you'll get much further with, say, western music theory if you know what is a major triad, and you can go much further with electronic music programming if you learn how to map numeric ranges.
hjh
-
-
Of course, just inverting the mtof, neat solution!
@bocanegra I agree, my mistake, actually what I made was the logarithmic one (the one the advances linearly in the frequency space) and I needed the linear one (the one that advances linearly in the midi notes space)
@ddw_music Nice, that is the type of solution I had in mind, but I was trying to treat the "signal" as the original line that goes from 48 to 84 and then aplying math to that, instead of considering the "signal" as a line in the domain [0,1] and then aplying math to map it to [48, 84]. I believe the general solution that I was seeking is the formula (1) in this answer: https://stackoverflow.com/a/63158920/4286437 (By the way, what I understood from bocanegra wasn't a superexponential, but just that the frequency as we hear, in the world of sensations, would rise in a logarithmic way when the frequency rises linearly)
-
@Cmaj7 there is an old discussion of the mtof (and ftom) math here: https://forum.pdpatchrepo.info/topic/4090/midi-to-hz-and-hz-to-midi-formulas/ - pay attention to @seb-harmonik-ar and @gsagostinho 's answers
The mtof formula written in simple math is
F = 440 x 2^((M-69)/12)or[expr 440*(pow (2, (($f1-69)/12)))]in pd lingo. It's not a superexponential (sorry @ddw_music I do agree on getting the mapping right tho). The 440 and 69 are sort of arbitrary in that they set a reference of Hz/Midnumber. You could just as well use 220 and 57 or any other pair you know to be correct, although keeping them sort of close to middle C is probably a good idea... -
@bocanegra Thanks, but the actual mapping between midi notes and frequency is not the original issue, which turned out to be just a matter of scaling. The question was solved by ddw_music, which is a particular case of the general formula in the stack link I sent (if you take x_0=0 and x_1=1 there you recover ddw_music formulas and more, you can take log(y) as any function f(y))
By the way, one related question regarding the implementation: are there performance differences between implementations with lots of [f ], [+ ], [t b f], etc ... and a simple [expr] or [expr~] ? Is one way preferable?
-
@Cmaj7 said:
By the way, one related question regarding the implementation: are there performance differences between implementations with lots of [f ], [+ ], [t b f], etc ... and a simple [expr] or [expr~] ? Is one way preferable?
Whithout any proof I will say this: when you load [expr] you load a shitload of functions in one object. I don't need pow, exp, sqrt, whatnot in order to do a linear transformation with 2-3 objects. You are also loading an "extra" which is not always supported in ports like libpd/mobmuplat depending on platform and version
-
I think using the built-in objects should be slightly more efficient for the basic cpu usage at least (dunno about memory usage or how that might influence cpu usage tho) since
[expr]implements its own call stack and uses a switch/case for every operator in every computation (whereas the single-function objects follow pointers to functions in classes). not sure how much more or less efficient that is.. of course[expr]is also far more convenient and clean from a language perspective.
tho btw, there is also a JIT expr compiler/external that should be just as fast if not faster than the vanilla many-objects approach
https://www.mail-archive.com/pd-announce@lists.iem.at/msg00234.html https://github.com/x37v/jit-expr
@bocanegra I thought that expr could be included in libpd and such now since the author permitted a license change. also since[expr]is in vanilla those functions will be loaded no matter what (the expr class owns those functions, not the object. And the class is loaded when pd starts)
edit: after testing it seems like the equivalent objects are 1 1/2 - 2 times faster than[expr] -
@seb-harmonik.ar said:
of course
[expr]is also far more convenient and clean from a language perspective.The funny contradiction here is that Max/Pd were supposed to make programming more approachable for people who don't like code, but the canonical way to write math in Max/Pd is... awful. It's really painful, and it's not any less fiddly than code in the end (perhaps even more fiddly, e.g.
1/x).Tbh I sometimes think this alone is enough to make graphical patching only a partially successful project. It's obviously successful in the sense that it appeals very deeply to a large number of people -- but can it be said to be easier than code? At first, yes, but perhaps not always so, in the long run.
hjh
-
@ddw_music agreed. there are some things that graphical programming makes really difficult, though it's generally more intuitive at first especially for audio imo
-
@seb-harmonik.ar said:
@ddw_music agreed. though it's generally more intuitive at first especially for audio imo
At some point, I realized that code requires you to have a mental map of the expected state at every step in the code sequence. Without this mental map, basically you're just throwing tokens at the wall and hoping something sticks. It's a little easier to visualize with patch cables, except for the ever-present risk of spaghetti patching (and this risk increases dramatically as algorithmic complexity rises).
But, though state is invisible in code, it scales up easily to very complex processes in a way that I don't see happen in patching very often. (Perhaps patching seems more intuitive because it implicitly discourages complexity.)
For audio, I'd agree in that new SC users do have trouble visualizing the signal graphs when they're specified in code. (But it's much easier to create large numbers of parallel chains in code, too.)
hjh
-
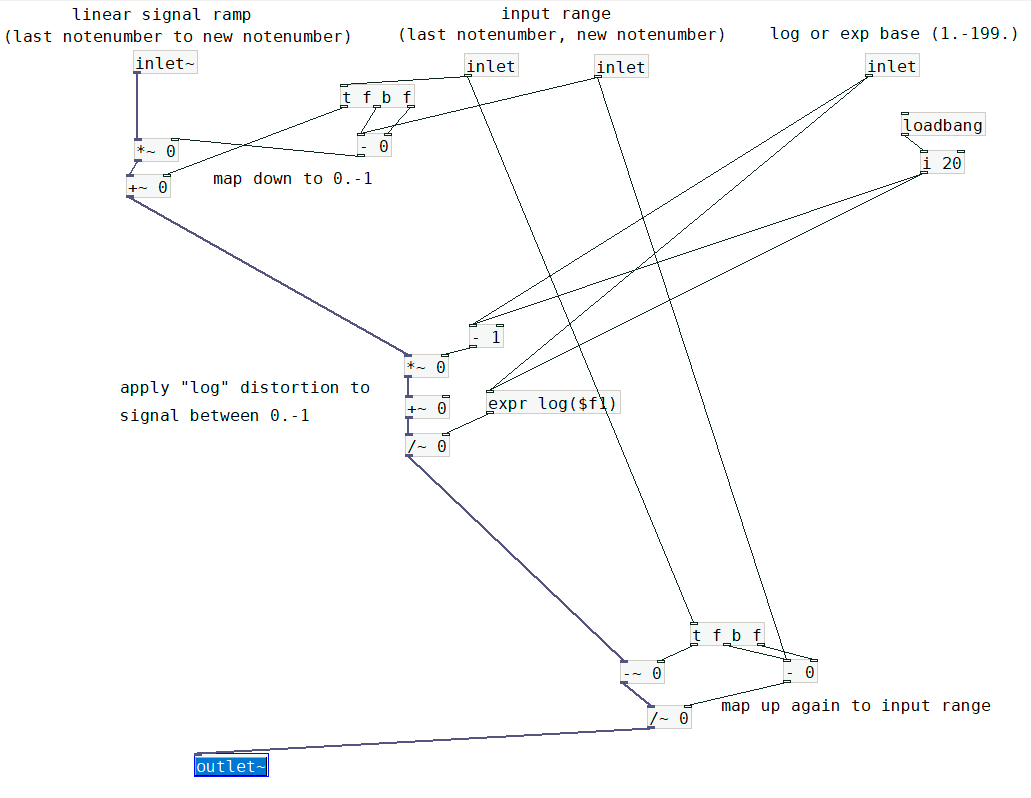
-
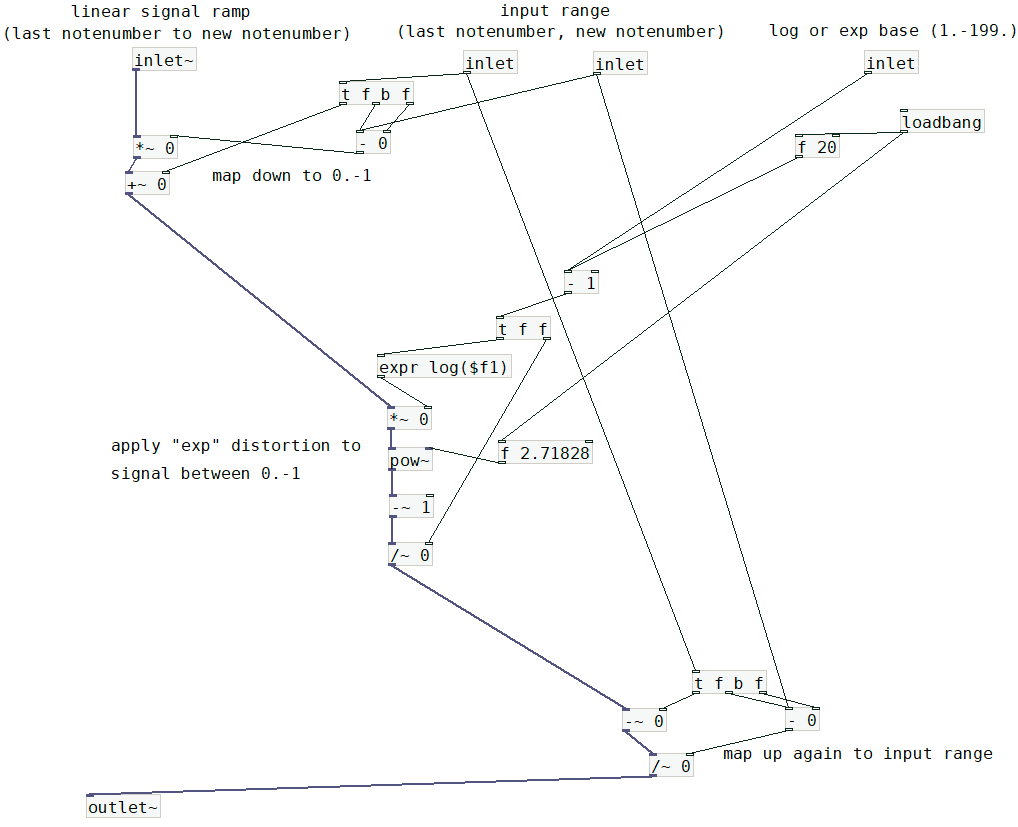
-
while using mtof and ftom gives you musically useful curves, these readymade objects do not really teach you how to perform arbitrary distortion of input ranges.
the screenshots above (untested, i just made this up from memory) will need to know the last note on notenumber and the current note on notenumber, and then it performs the following tasks:
-
scale the (linear) input range (in note numbers) down to 0.-1.
-
perform a distortion on that linear range of 0.-1.
-
scale back to the note numbers you need.
-
-
it is always good practice to
-
do anything you do to frequency (vibrato, pitch wheel, randomisation, offsets and transpositions, relational functions, range distortion for portamento effects) on the linear layer
-
as soon as it is unavoidable, go to signal domain
-
then use mtof~ only "inside" the oscillator /generator.
because, beside other things, it is easier to think in note numbers than in hertz.
-
-
oh yes.
and to get the inverse direction of the distortion, simply inverse that 0.-1 range by * -1, + 1, one time before the distortion function, and one time after it.




