I'm trying to find a better and more sophisticated idea for the algorithm. We need to find the number of samples in a period and then randomly choose where to place it. The problem is that if we do this explicitly this way, it doesn't seem to work well for a dynamically changing frequency input at audio rate... trying to find a way here...

@porres said:

I'm trying to find a better and more sophisticated idea for the algorithm. We need to find the number of samples in a period and then randomly choose where to place it.

I'm not in C, but I think I kind of did exactly that in my latest version, trying to solve the problem with non-integer periods. Here it is (commented in the patch) ...

velvet-noise.pd

Could certainly be optimized in some ways (especially using ELSE objects). But does it even work? I don't have a good method to test it, unfortunately.

@manuels said:

Could certainly be optimized in some ways (especially using ELSE objects). But does it even work? I don't have a good method to test it, unfortunately.

nice! - i like this counter for samples per phase:

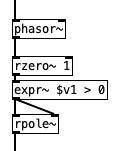
... from what i tested: it behaves perfectly well up to nyquist - although also in this range, there are sometimes consecutive non-zero samples (which i'm still not 100% sure if valid. see the 1, 1 in the middle below. the blue graph is the scaled offset per phase).

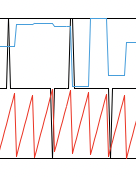
@ben.wes Thanks again for testing, really helpful!

Yes, it's true, that I didn't care about consecutive non-zero samples. For now I'm not sure what's more important: to comply to this constraint or to behave properly above nyquist.

The problems with frequencies above nyquist, that you found, probably have to do with the representation of small floating point numbers. I should have used [expr~ int($v1)] to get real zero values. Can't fix it right now, but I'll try tomorrow ...

@manuels said:

Yes, it's true, that I didn't care about consecutive non-zero samples.

Is there a rule not to have consecutive samples? If so, Nyquist is the limit

Ok, I changed the algorithm a bit and now I think I nailed it and solved it for frequencies up to Nyquist and above! I'm just randomly choosing any sample in the period, from first to last and I don't have if there are consecutive samples, like the last sample from the previous period and first sample from the current one.

    for(int j = 0; j < x->x_nchans; j++){
        for(int i = 0, n = x->x_n; i < n; i++){
            double hz = in1[j*n + i];
            double step = hz * x->x_sr_rec; // phase step
            step = step > 1 ? 1 : step < 0 ? 0 : step; // clip step
            t_float imp = 0;
            t_float r =  x->x_rand[j]; // - step;
            if(phase[j] >= r && ((lastphase[j] < r) || (x->x_1st[j])))
                imp = velvet_random(x) > 0.5 ? 1 : -1;
            out[j*n + i] = imp;
            x->x_1st[j] = 0;
            if(phase[j] >= 1.){
                x->x_1st[j] = 1;
                x->x_rand[j] = velvet_random(x);
                while(phase[j] >= 1.)
                    phase[j] -= 1; // wrap phase
            }
            lastphase[j] = phase[j];
            phase[j] += step;
        }
    }```

ok, just implemented bias and regularity as well... which was really a no brainer, cool! I like how I can turn this into an impulse oscilator if I set the regularity to maximum and bias to a single polarity. Then we can just introduce a little bit of randomness in both cases.

Wow, this is a pretty cool object and random noise generator. Thanks everyone who participated

I will announce when I officially include this object, I might squeeze this one in for the next upcoming release in a week or so

having the object at full sample rate frequency and then adjusting the bias to a low value, just so a few of the samples are of an inverse polarity, also creates a nice texture!

Done!

Now for the big question, where are the Reverb algorithms based on velvet noise?

here's the code, object should be in the next release any time now, just need Tim to help me compile a few things... https://github.com/porres/pd-else/blob/master/Code_source/Compiled/audio/velvet~.c

thanks again

So here's the fixed version: velvet-noise-fixed.pd

It wasn't just the issue with small floating point numbers, but more importantly it now didn't work with integer periods. In this case, of course, the period must never be reduced by one sample!