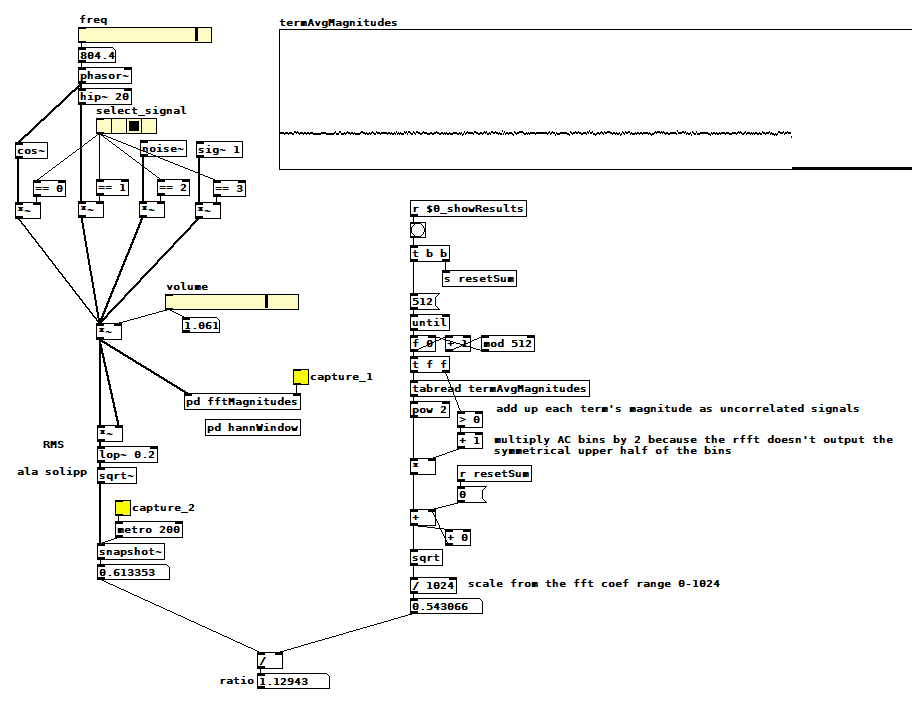
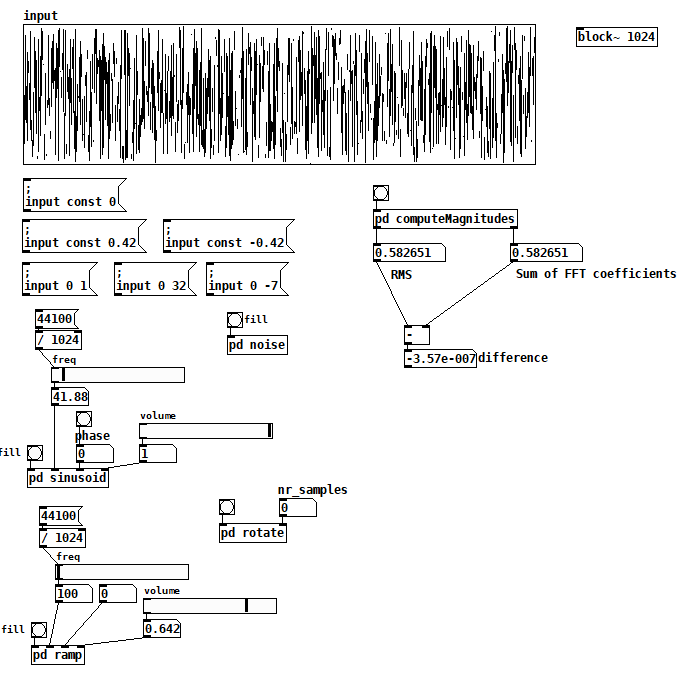
If it turns out to be possible to measure how much a signal aliases using an oversampled FFT I think I need to know how to sum the complex magnitudes of an FFT and how that sum relates to the signal's RMS amplitude. I'm trying to figure it out with this patch: compareTimeFreqAmpl.pd . 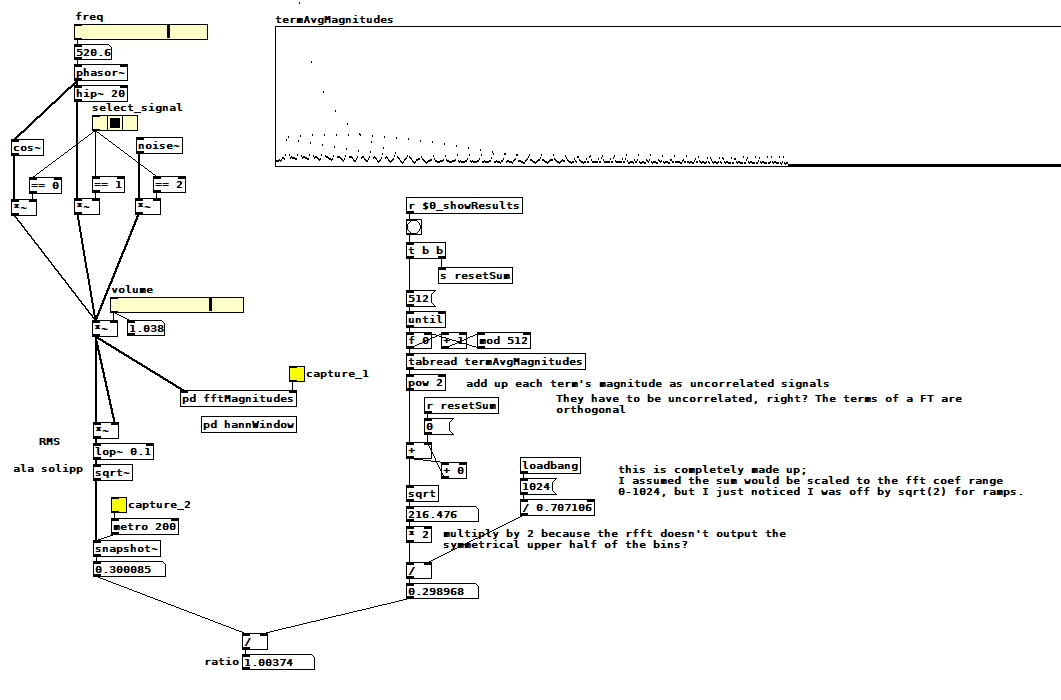 Select one of the three signals, pick a frequency if applicable, pick a volume, then capture the average magnitude of each FFT term (it computes the magnitude of the sum of all terms when you clear the capture toggle). Next, capture the RMS amplitude, which displays the ratio between the two measurements as a side effect. I hacked the ratio to be close to 1 for cos~ and ramps, but it's ~1.125 for noise. Note that I'm not using a hann window inside the fft subpatch--I think it's not relevant to this problem, and it seems to only change the ratio by 3/2, which is the expected effect of a hann window with 4x overlap.
Select one of the three signals, pick a frequency if applicable, pick a volume, then capture the average magnitude of each FFT term (it computes the magnitude of the sum of all terms when you clear the capture toggle). Next, capture the RMS amplitude, which displays the ratio between the two measurements as a side effect. I hacked the ratio to be close to 1 for cos~ and ramps, but it's ~1.125 for noise. Note that I'm not using a hann window inside the fft subpatch--I think it's not relevant to this problem, and it seems to only change the ratio by 3/2, which is the expected effect of a hann window with 4x overlap.
You can see my ratio hack in the divide operation just before the ratio computation. I saw that I was off by sqrt(2) so I just included it, but is it sqrt(2), and if so, why? Why is noise different? Is it right to sum the FFT term magnitudes as uncorrelated signals? Is it right to double the sum because the rfft skips the symmetrical upper half of the terms for efficiency? What else am I doing wrong?
Edit: Hmm, that symmetrical upper half of terms? Probably uncorrelated as well. So the doubling has to happen before the sqrt, and then you get...sqrt(2)! Is that plausible?


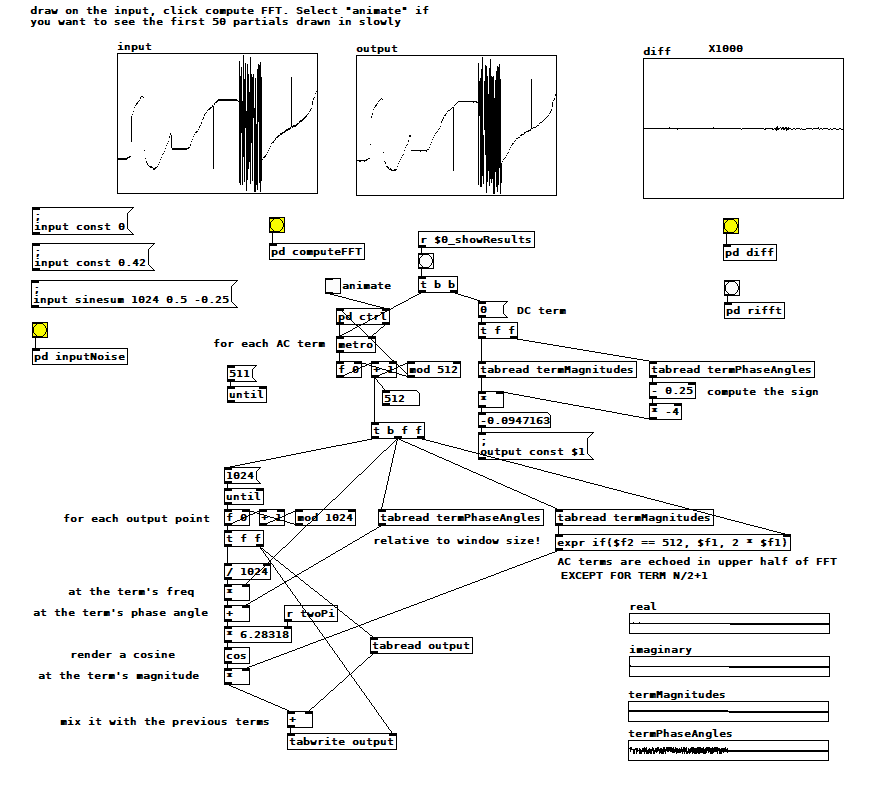
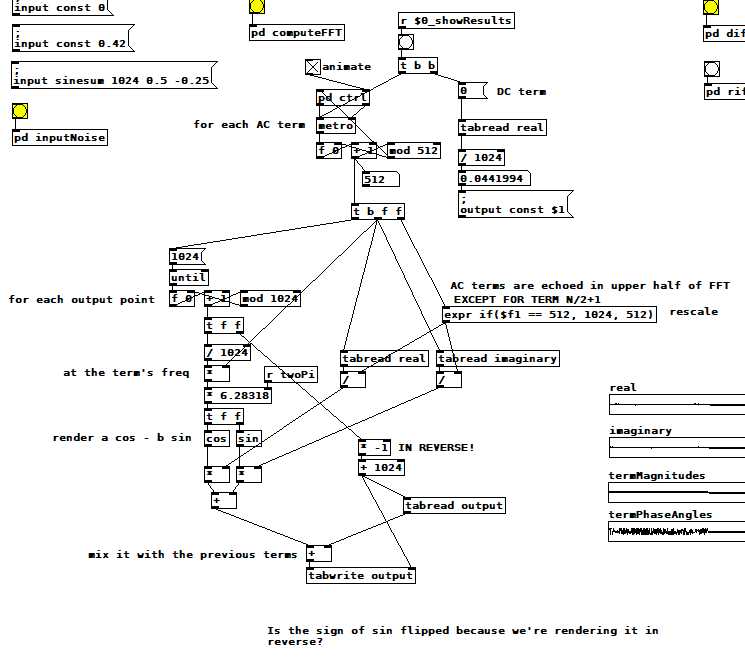

 Inside [pd computerMagnitudes]:
Inside [pd computerMagnitudes]: 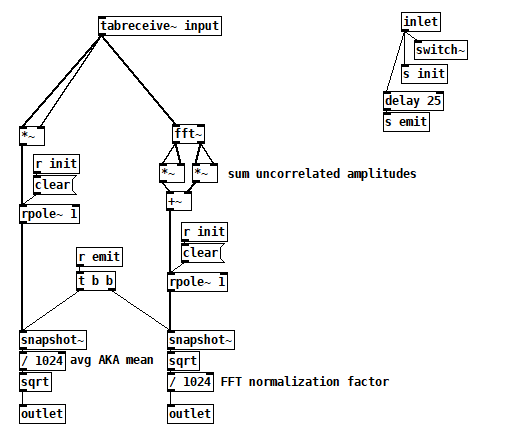
 IMHO, this contradicts what she spent so much effort establishing on the prior two pages (
IMHO, this contradicts what she spent so much effort establishing on the prior two pages ( In this case I agree--Fourier coefficents are really the peak amplitudes of the cos and sine components--but my confusion over this is what made me program the patch the way that I did. So why is it working?
In this case I agree--Fourier coefficents are really the peak amplitudes of the cos and sine components--but my confusion over this is what made me program the patch the way that I did. So why is it working?