Hi all,
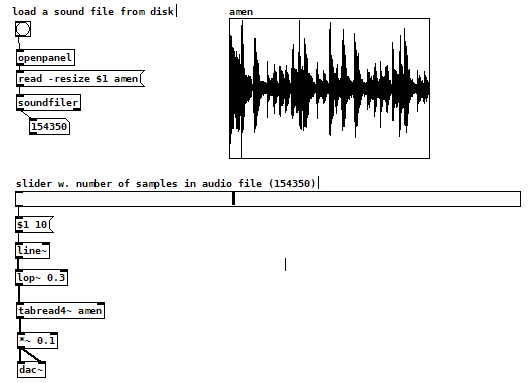
could someone be so kind as to explain the workings of the lop~ object in this patch to me?
This is a "simple" scrubbing bar that let's the user "scrub" through the loaded audio file by moving the horizontal slider. The lop~ was inserted to make this specific kind of "tape-start" / "tape-stop" effect that is familiar from some DAWs and DJing software.
It's hard for me to even formulate a question properly but it revolves about the fact that a filter object that usually is used for frequency-domain tasks (for example filtering high frequencies out from an audio stream) in this case is used as a time-domain-effect, i.e. creating a certain start-up / slow-down effect. I can't get my head around this. What's also confusing / interesting is that when you monitor the number outputs from the line~ and the lop~ with a snapshot~ object every 1ms the lop~ will output different numbers for some time while the line~ has already stopped outputting anything. How come? What does that mean for when you actually use lop~ as a "classic" audio filter to low-pass, say, a mic input or instrument recording.
I hope my question / confusion is somehow comprehensible. I am highly grateful for any explainations, preferably in layman's terms 
oyster
p.s.: the patch is from Andy Farell's super interesting lecture on Microsound - Granular Synthesis - Physical Modelling - Procedural Audio which I'm trying to follow along. youtube.com /watch?v=Qxqtc2bgDpw




