This might be a stupid question, but I'm wondering if there is another way of dealing with complex output signals than just taking one of the parts as a real signal.

So to make clear what I mean by "converting" a complex to a real-valued signal, let's take the (complex) output of [vcf~]. Unsurprisingly, neither the real nor the imaginary part corresponds to the calculated frequency response of a one-pole complex filter. My question could then be asked in the following way: How do I get a real-valued signal with that same frequency response?

In the following patch, I tried to "convert" the complex output of [vcf~] to a real-valued signal (ab)using FFT. I'm not sure if it's possible to combine a complex FFT with a real IFFT in such a way, but it kind of seems to do the job ... vcf-test.pd

Does anyone know a better method for this?

@manuels Such an interesting question. I don't really know, but maybe you want to start by converting the complex signal from cartesian to polar coordinates? I think the instantaneous frequency would be related to the absolute value of the rate of change of the angle, and the instantaneous amplitude is just the magnitude.

@jameslo Yes, maybe that's a good starting point. If I get it right, converting the complex signal from Cartesian to polar coordinates would somehow correspond to the "analytic" part of what FFT does in my example. But I have no idea how I could use this to (re)synthesize a real-valued signal ... This is all way over my head, I guess. Thank you anyway!

I just found an easier way to do it: Just make a (relative) 90 degree phase shift between the real and imaginary parts and add them! For better understanding I use the original [hilbert~] object instead of building a new one out of its two biquad filter sections. vcf-test2.pd

@manuels a complex-valued signal will have both a real and an imaginary part. therefore the output of vcf~ does actually correspond to the frequency response of a 1-pole complex filter, because it is the complex output of a complex filter.

It is just when you take the real or imaginary parts separately they have the frequency response of a 2-pole filter (see miller's book for hints on the math involved).
http://msp.ucsd.edu/techniques/latest/book-html/
And this is the useful thing because you can't really "hear" a complex signal, the complex signal is simply a way to keep track of phase with vector-like complex numbers. Sound channels only have 1 dimension (and usually we use "real" signals for this)

usually in order to "make complex filters real" the method is to pair each complex pole or zero w/ its conjugate afaik. But vcf uses some other tricky math

@seb-harmonik.ar Thanks! Yes, I'm aware of this technique "partial fractions", and there is nothing wrong with [vcf~], of course!
It's just that in some cases the conjugate poles have quite undesirable effects (especially at low frequencies), and so I wondered if there are useful alternatives to the common pairing of poles an zeros ...

Isn't the real signal the norm of the complex one?

If complex signal is a(t) + i*b(t) then norm is sqr(a²(t) + b²(t))

@manuels said:

Just make a (relative) 90 degree phase shift between the real and imaginary parts and add them!

I think that only works for positive frequencies, e.g. broken for negative frequencies.pd
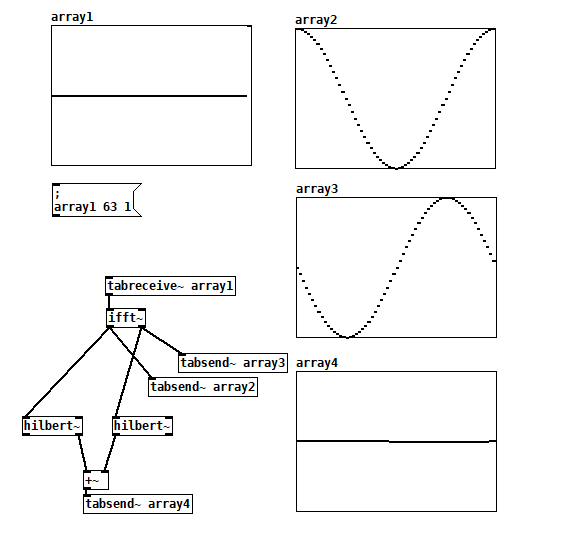Edit: hmm, but it looks like your fft~/rifft~ scheme also fails on this example. Is it also broken, or is my reasoning broken?

@FFW said:

Isn't the real signal the norm of the complex one?

I don't think so. In the negative frequency example I just gave above, the norm is a constant 1.

@FFW the norm is a real number but that's the "magnitude". the real part of the number itself is the "horizontal" (non-imaginary) component of the complex number

@jameslo said:

Edit: hmm, but it also looks like your fft~/rifft~ scheme also fails on this example. Is it also broken, or is my reasoning broken?

Well, I wouldn't be too surprised if both of my attempts turn out to fail ...

While we're at it: Can anyone explain the "ampcorrect" of vcf~ which, according to the source code, is 2-2/(q+2)? Maybe this is related to the original topic, because it means that what I incorrectly called the "sum" of real and imaginary output is limited to 2 (instead of the real output gain being limited to 1, which it actually isn't).