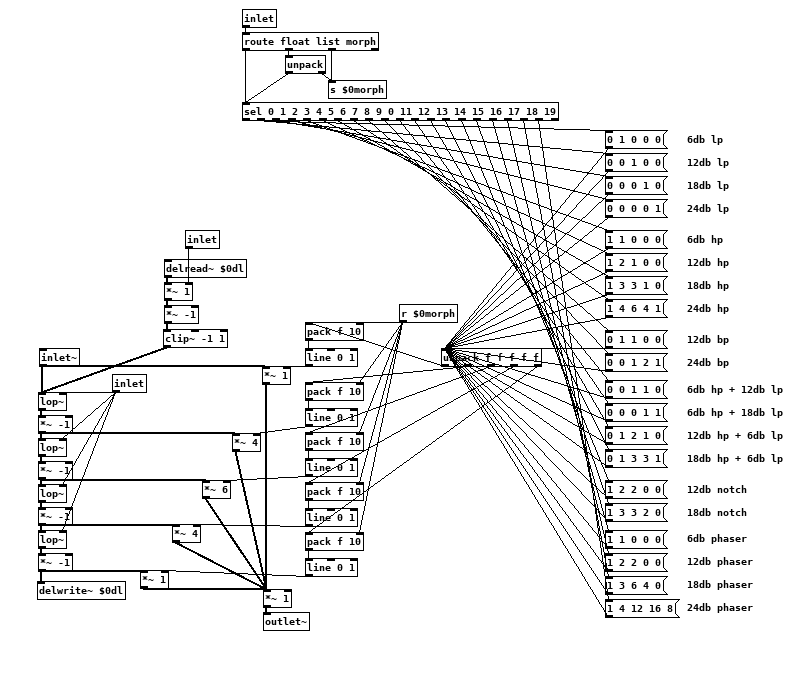
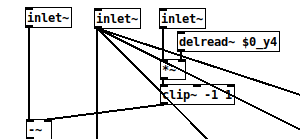
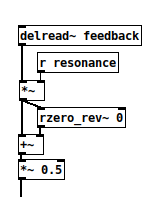
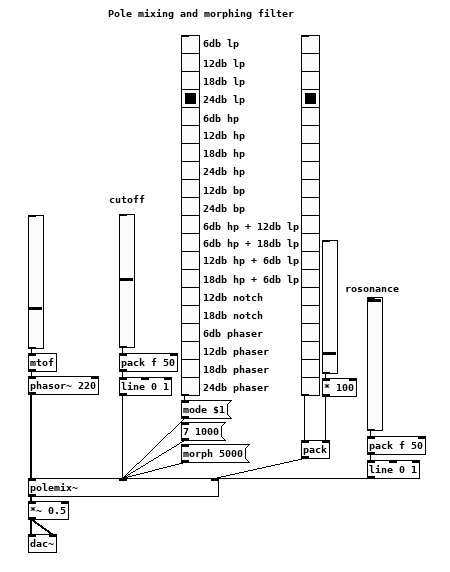
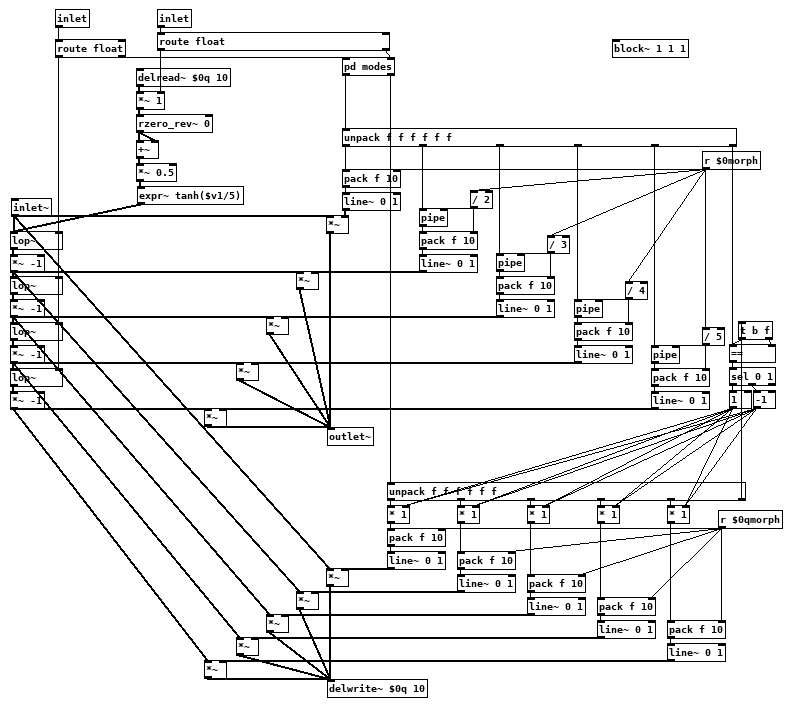
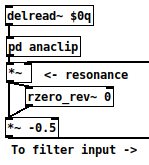
@oid It's getting better and better! The tanh soft clipper adds a nice grit to the sound 
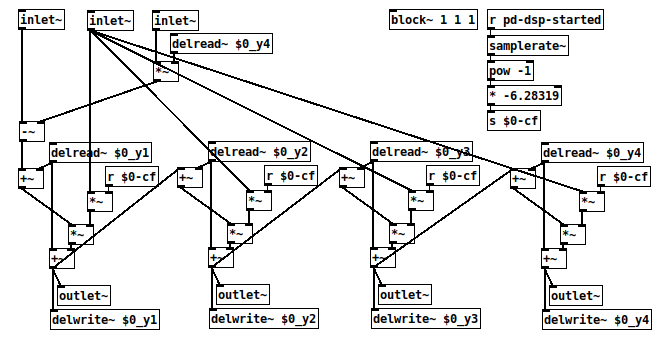
Is there a specific reason for setting the feedback delay to 10 samples? I would think 1 sample delay to be ideal?
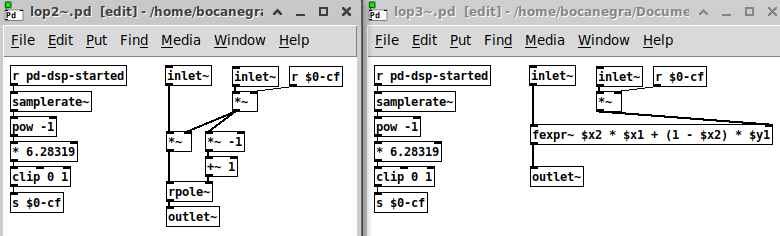
I still prefer having signal rate frequency control. There are several ways to achieve this besides the filter I posted previously. The classic one pole low pass equation is y[n] = y[n-1] + a * (x[n] - y[n-1]). That was what I based my filter on (with a few tricks to minimize computation exploiting the fact that each filter should also be inverted). You could do this with [fexpr~] as well (and [rpole~] too).
Testing impulse response against [lop~] there is a slight difference (very tiny) in output amplitude, which I reckon is either because of difference in filter coefficient calculation or [lop~] gaining the outlet slightly as mentioned in H01.low.pass.pd: The lop~ object is normalized to pass DC (the lowest frequency) with a gain of one
However, looking at the source code for [lop~] ( https://github.com/pure-data/pure-data/blob/master/src/d_filter.c ) the coefficient is calculated the same way as I did it though: coef= F(Hz) * 2PI / samplerate. I can't seem to find any "normalizing" function, and the central filter equation is: y[n] = a*x[n] + (1-a)*y[n-1], essentially the same as y[n] = y[n-1] + a * (x[n] - y[n-1]).
Here are two [lop~] alternatives with signal rate frequency input for you to try out: Alternative_lop.zip