@EMR66
A couple of illustrations.
Let's say we want a sine wave covering 16.5 samples. To illustrate, I used SuperCollider to put two sine wave cycles into 33 samples.

The second cycle begins when the wave crosses the 0 line in the middle.
This is between samples.
So, the second cycle must be represented by sample values that are different from the sample values for the first cycle.
That is, it is possible to have that zero crossing between samples -- but the sampling process produces different values.
Let's look at it a different way: blue samples = one sine wave cycle covering 33 samples; green samples = 2 cycles in 33 samples.
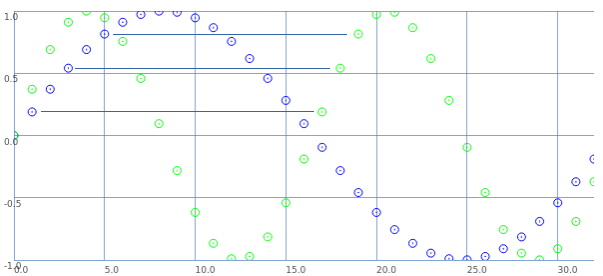
If we start counting samples at 0:
- Blue 0 = Green 0.
- Blue 2 = Green 1.
- Blue 4 = Green 2. etc.
That is: read through the blue samples at double speed, and you get the 16.5 wavelength. (This is exactly what David said.)
What about the second cycle starting at 16.5?
- Blue 1 = Green 17.
- Blue 3 = Green 18. etc.
These are the sample values that were skipped the first time.
So, Green 17 (the first concrete sample value after the second cycle begins) is the value in between Green 0 and Green 1. Green 18 is in between Green 1 and Green 2.
This is interpolation.
Interpolation is the mathematically correct way to represent fractional cycles in a sampled signal.
You can try to say that this "isn't the real problem," but... this is the problem, and interpolation is the solution.
hjh