Here is my attempt:
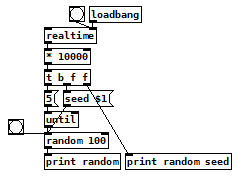
It works okay (at least there is some variation), but I think the problem is that there is an average time for [loadbang] so the probability for some numbers is higher then for others.
Best way to create random seed on [loadbang] with vanilla?
Here is my attempt:

It works okay (at least there is some variation), but I think the problem is that there is an average time for [loadbang] so the probability for some numbers is higher then for others.
@Jona Very interesting, thank you! 
@Jona Yes, when i just print it, it starts with high numbers and goes down to lower numbers... Confusing 
print: 1557
print: 2072
print: 1565
print: 1291
print: 1523
print: 967
print: 840
print: 694
print: 692
print: 717
print: 720
print: 800
print: 696
print: 701
print: 681
print: 688
print: 1023
print: 691
print: 687
print: 690
print: 690
print: 699
print: 680
print: 690
print: 696
print: 690
print: 703
print: 816
print: 645
print: 641
print: 635
print: 635
print: 635
print: 671
print: 645
print: 643
print: 658
print: 653
print: 644
print: 669
print: 644
print: 641
print: 644
print: 641
print: 886
print: 936
print: 747
print: 691
print: 691
print: 731
print: 707
print: 635
print: 703
print: 650
print: 644
print: 645
print: 675
print: 645
print: 653
print: 645
print: 645
print: 645
print: 670
print: 650
print: 774
print: 714
print: 718
print: 694
print: 700
print: 690
print: 756
print: 650
print: 689
print: 991
print: 702
print: 718
print: 690
print: 691
print: 690
print: 694
print: 644
print: 787
print: 937
print: 644
print: 669
print: 684
print: 644
print: 649
print: 649
print: 648
print: 667
print: 650
print: 686
print: 736
print: 1007
print: 645
print: 678
print: 645
print: 645
print: 645
Dynamic patching also looks promising: random-test4.pd 
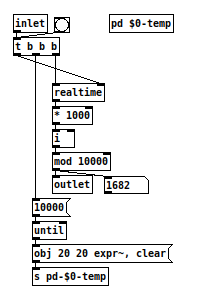
Just another thought on [random2]: It cannot be ruled out that it runs into a loop. I tested that a seed never produces the same number, but it can happen that a seed produces a random number that is used as the next seed that produces the previous seed – or that it happens later in the process. I could test it to some depth, but it is not feasible to test it for millions of random lines.
So it is probably better to go with the entropy approach. 
If you have a seed range up to 10.000 you have 10.000 possible lines of deterministic random numbers and some may appear more often or even sometimes repetitions may appear, but there is not the possibility of an actual loop. 
Also if you would use [random2] in a patch and publish it, the patch would behave exactly the same for anybody who downloads it. It would not be recognizable by anybody, as it would seem to be random – but from a more holistic standpoint it would diminish the total results the patch could provide on a universal level. 
Anyhow, it was very much fun writing it. 
And with the entropy approach you can decide to reseed [random] at any time – possibly with entropy gathered from user interaction – to break out of the deterministic behavior 
also interesting that, if you would use epoch time for the seed, the result should be totally deterministic even if the time never repeats.
now it depends on knowing the seeding algorithm to find out what numbers will return with a certain seed...
but still it should seem totally random if not knowing the time and the seeding algorithm.
if using lua you do not even need [random] for that. i implemented epoch time with millis for ofelia once,
auto duration = now.time_since_epoch();
auto millis = std::chrono::duration_cast<std::chrono::milliseconds>(duration).count();
https://stackoverflow.com/questions/9089842/c-chrono-system-time-in-milliseconds-time-operations
but for now the seed it is generated from ofGetElapsedTimeMicros():

@Jona Yes, i believe at the core of each random algorithm is a cryptographic hash algorithm. A hash algorithm provides an output for each input in such a way that you cannot determine the input if you only know the output, even if you know the algorithm.
The only way to determine the input would be by brute force, that means calculating the outputs for all possible inputs within a given range and storing all input-output pairs in a huge so called rainbow table. With that you can look up the input for any output.
But other than that you cannot for example see any connection between hash(12) and hash(13). The inputs are close together, but the outputs are completely distinct.
With this you can generate a chain of numbers that seem completely random but are in fact mathematically determined. Only if you add outside unpredictable information, entropy, to the mix, the results can become truly random. Or at least have a random starting point if the entropy is added only in the beginning.
For actual cryptography it is crucial to get good entropy into the system, as the algorithms are usually known and well researched and every bit of information about the starting condition can help to decipher the encrypted code.
But for Pd purposes it doesn't have to be that complicated. The actual time would be enough, if only Pd had an object for that.  In one of the examples above [time] from zexy was used. But again, there is the problem with raspberry pis that don't have internet access. They don't have a battery to keep a clock running when they are off, so they always start at the same date after booting. So of course you would have some different time after Pd has started, but it is not as reliable as it would seem at first glance.
In one of the examples above [time] from zexy was used. But again, there is the problem with raspberry pis that don't have internet access. They don't have a battery to keep a clock running when they are off, so they always start at the same date after booting. So of course you would have some different time after Pd has started, but it is not as reliable as it would seem at first glance. 
So a simple random generator would just do hash(seed), hash(hash0), hash(hash1) and so forth...
And some modulo to get into the desired range. 
Oops! Looks like something went wrong!