Hi everyone.
I use the [struct] and [pointer] objects to store datas from a CSV text file (by using the [textfile] object).
I never had problems before, but I just discovered that it's not possible to store more 248 lines of datas.
Is there a way to increase this limit, or another way to store datas without limitation?
Thanks in advance if you can help.

@jancsika

I've been thinking more about recursion and the "unrolling" problem that leads to memory spikes. Am I right in thinking that recursive patches (ie. patches where an outlet is attached to a hot inlet upstream) can be equally as efficient as using [until] if you get the trigger order right?

Here's an example:

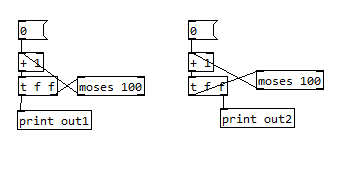
In the first example, PD has to stack all 100 calculations before prints out any one of them. But in the second it can print and "forget" them one by one. Is the second version theoretically just as efficient as using [until]?

(Note that creating a line of numbers is not the problem I'm trying to solve here. I'm just using a simple example for illustration.)

@LiamG You will still get stack overflow if you choose a higher number for moses. I believe that is because pd puts the floats on a stack before actually printing and deleting them and tries to finish the computation first until the stack is full.

Yes, as Jonathan explained, PD tracks recursive operations and spits out the error message when a certain limit is reached, in order to avoid stack overflows. Obviously there are better ways to perform the operation above, but I'm still wondering if the second one is theoretically just as efficient as using [until].

@LiamG Yes, both of your versions work (the first one prints reverse order). But if you try it with [moses 1000], both will likely break. Whereas with [until] you can easily count up 1000 times:

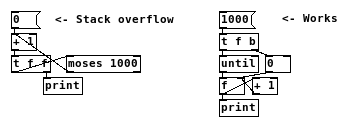
That's right. What I want to know is: do the two options that you have described use memory in the same way, or is one more efficient than the other? In other words, I want to know if the "stack overflow" message is pointing to an actual spike in the memory.

@LiamG i don't know that for sure, but i would guess so. But the stack is so small that it should not be relevant in terms of computer ram. What i observed once is that the print function seems to be internally disconnected to the actual computation so that the printout on the console can occur with some actual delay.

@LiamG The "stack overflow" message results from a simple counter-- when you send to an outlet, a generic outlet handling function 1) increments the counter, 2) forwards the outgoing message to the objects that are connected to that outlet, and finally 3) decrements the counter.

In the first chain you've initially got three objects involved in the recursive call, each of which adds an iteration to the loop. When the incremented value finally hits the target, you print out the value in order from last iteration to the first.

In the second chain, you've got four objects, but one returns before the leftmost "f" of the trigger starts the next iteration of recursion. So in that case you print out starting from the smallest value to the greatest.

As for which is more efficient, I'm not sure.

Thanks for chiming in @jancsika. You confirmed what I thought about the "stack overflow" counter. Pondering the issue more, I think what I am trying to get at is the difference between memory overflows and CPU overflows. These seem like very different things, although they are covered by the same error message. I'm going to elaborate my question, because I suspect that you do know the answer, if only I can communicate clearly.

My intuition tells me that the first example I posted uses a lot more memory than the second, precisely because it has to remember the numbers 0-98 before it gets to print anything. If the process continued for long enough, it would lead to a memory overflow, ie. the stack would be required to store more numbers than its capacity allows. This is what the "stack overflow" counter is there to protect against.

In the second example, however, the memory overflow doesn't seem to enter the picture. The number is forwarded to the print object and "forgotten" before it is sent back to the top. So if the second example were run without [moses] or any other safety limit, it would not eat up the memory. It would, of course, lead to a CPU overflow, since the process would never terminate, and the computer would still crash if the "stack overflow" counter failed to intervene. But it would crash for a very different reason than the first example, ie. because of a CPU overflow, not a memory overflow.

Does my reasoning here seem correct? Is there anything I've overlooked?

I'll now give some context to my question, because you're probably wondering why I care so much about these details. The context is Context, the library that I'm building. Context uses a lot of recursive functions similar to the second example that I posted, and I'm trying to decide whether or not it's worth rebuilding them using [until]. This would be a lot of work, but there are two reasons why it might be worth doing: 1: Because it would make Context more efficient, and 2: Because recursion will lead to unwanted error messages, as @ingox pointed out.

I am currently much more interested in 1 than in 2. For whatever reason, unwanted error messages have not been a problem for me so far (perhaps because I haven't reached the limit). As for efficiency, the standard answer seems to be that it doesn't make an appreciable difference on modern computers, but in fact I am finding reasons to care about it. Context has a heavy loading procedure, involving several recursive algorithms of the type I've outlined in the second example. Load time is something I care about because it can lead to audio dropouts, hence I am trying to decide whether or not I need to replace my recursive systems with iterative [until] based systems. I ran a simple test* for one such system and found that the recursive system actually seemed to run faster than the iterative counterpart, contrary to what I had expected. This makes me inclined to stick with recursion, but I'd like to know if there is anything that I have failed to consider.

*I can provide more details about this test you like, but I'm worried that if I do so now it would lead to a memory to overflow!

Does my reasoning here seem correct?

It doesn't.

Both loops will cause a stack overflow if you get rid of the recursion limit altogether and recompile Pd. You can probably figure out a dynamic patching hack to elucidate this-- for each trip through the wire connection that feeds back into the chain, copy and paste that part of the chain and add it to the canvas. When you're done you'll see how many objects you had to traverse in order for the recursion to work. (This has the added effect of increasing memory on the heap, which doesn't happen with the recursive loop, but under normal circumstances that shouldn't matter. Your memory limits for the stack are much lower than the heap.)

In a compiled language like C, the compiler can take a pattern like your 2nd chain and re-arrange it into a functionally equivalent iterative loop-- this is called tail call optimization. Even Javascript now has that as a feature. But Pd has no such feature, nor any feature really to optimize computation across a chain of control objects.