Hello there, is there a way to go through all possible permutations with repetitions of given data? for example, I have 16 slots for harmonics and each letter represents a different percentage in volume from 0 to 100%, "e" could represent 13% if you want: (a,b,c,d,e,f,g,h,i,j,k,l,m,n,o,p). Im using Iannix to control Pure Data so I imagine that in iannix when the curve is at the top it will start with all possible combinations and permutations with repetitions and when the curve is at the bottom it will end, and have gone through all possible combinations.
Im aware of the number of combinations possible and their vast space, with 5 slots for harmonics with a,b,c,d,e for volume, with its repetitions and permutations I got 3126 different combinations or timbres.
For example: the category for using 5 harmonic slots with 4 different volumes and one repetition of volume is this:
(if you have repetitions one letter will be left out)
1.-aabcd 2.-aabdc 3.- aacbd 4.- aacdb 5.- aadbc 6.-aadcb 7.-abacd 8.-abadc 9.-abcad 10.-abcda 11.-abdac
12.- abdca 13.- acabd 14.-acadb 15.-acbad 16.- acbda 17.-acdab 18.- acdba 19.-adabc 20.- adacb
21.- adbac 22.-adbca 23.-adcab 24.- adcba 25.-baacd 26.-baadc 27.-bacad 28.- bacda 29.-badac 30.-badca
31.-bcaad 32.- bcada 33.-bcdaa 34.-bdaac 35.- bdaca 36.-bdcaa 37.-caabd 38.-caadb 39.-cabad 40.-cabda
41.-cadab 42.-cadba 43.-cbaad 44.-cbada 45.-cbdaa 46.-cdaab 47.-cdaba 48.-cdbaa 49.-daabc 50.-daacb
51.-dabac 52.-dabca 53.-dacab 54.- dacba 55.-dbaac 56.-dbaca 57.-dbcaa 58.-dcaab 59.-dcaba 60.-dcbaa
Ultimately Id like to use 32 harmonic slots with 32 letters for volume or maybe 10 letters for volume with 32 harmonic slots, is there an algorithm to this?
Can someone help me?!
Thank you!
-
all possible permutations with repetitions of harmonic volume from top to bottom
-
@Pándinus In traditional languages the permutation problem can be solved with very little code using recursion. In Java: https://stackoverflow.com/questions/4240080/generating-all-permutations-of-a-given-string. There are also solutions without recursion (Heap’s algorithm).
I tried a little bit to implement the Java example in Pd, but couldn't get my brain to wrap around it yet. There is an excellent example of data flow recursion in iem [list-drip] of the list-abs library. Therefore i guess that there must be a very elegant way to do it.

-
@ingox Ok im doing research on Heap´s algorithm now, let me know if you can advance this, from what I can tell heap´s algorithm includes repetitions right? if it interchanges a single pair of elements...
"bbbb" with 0 permutations, but bab with 3 (abb,bab,bba).
If two elements are the same like bb, it would skip them and move on to where there are two different elements to eliminate redundancies... like in the previous example bbbb would have 0 permutations instead of 24 permutations.
The repetitions are very important since in this exercise they will create a ton more of different timbres.

-
I can think of a rough outline of a PD patch that might do this, although I haven't worked out any of the details. It would go something like this:
- Make an abstraction which converts base 10 numbers to base 32 numbers, ie. 9 --> 9, 10 --> a, 11 --> b ... 32 --> 10. (not sure how you'd do this but it must be possible).
- Interpret the output as a symbol and expand that symbol into a list of characters, using either [s2l] or [list fromsymbol].
- Iterate the list and look for repeating characters. If a character repeats exactly twice, accept it, else reject.
Step 1 is the hardest part; the rest is fairly trivial. Once this is built, you can iterate through as many (decimal) numbers as you like using [until] or [uzi].
-
@LiamG Thanks! Ill try!
-
For step 3, I think that the easiest way of doing this would be to use arrays. You can use [array max] to search for the largest number in an array, and then set that index to 0 using [array set]. Next, query and remove the next highest value, using the same process. If the second highest value is the same, then you know there is a repeat. Like this you can check to see if there are 2 instances of a particular number in a given list.
Of course, using arrays requires that the list in step 2 consists of only numbers, not symbols. I have some ideas for achieving this too, which I can share if you decide to take the approach I've described.
-
@LiamG Ill try to implement Heaps algorithm, but it will take me some time, Im a beginner
-
@Pándinus This could be one implementation of Heap's algorithm in non-recursive format. I took the example from https://en.wikipedia.org/wiki/Heap's_algorithm. This only works for lists of floats.
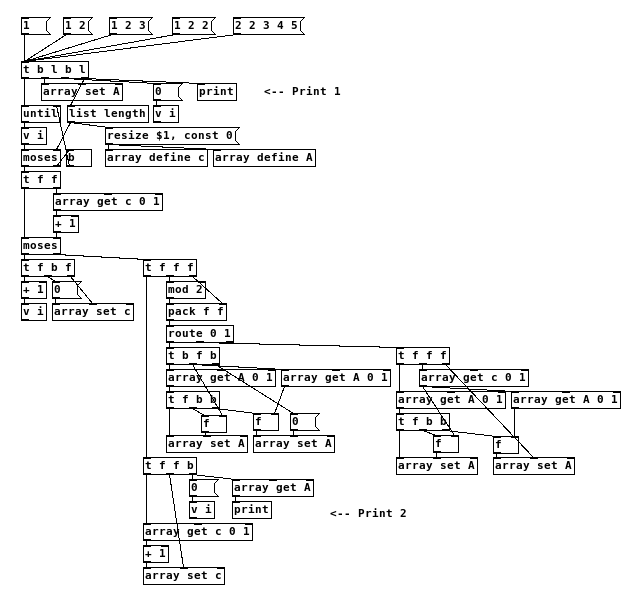
Heaps_algorithm.pd -
As i understand it, Heap's algorithm doesn't look for repetitions, only for positions. Therefore 1 2 3 has six permutations, as well as 1 1 1 has six. But i didn't got to understand the algorithm completely, just tried to make an implementation.

-
Hi,
I'm not sure if this is what you are after, and it's quite slow for longer lists because it uses a very fast [metro] instead of [until] (which crashes pd for some reason), but it works with symbols as well. At the end it creates a text file with the name of the input list in the patch folder with one permutation per line.I hope it's of any help.
-
Actually my patch doesn't work with repetitions (a list of '1 1 1' doesn't even give 1 permutation but instead it just loops forever trying to find a new permutations).
I think that a way to do it would be to convert the original list to unique floats (so that list 'a b c' becomes '1 2 3'), get all the permutations of that and then scan each permutation and convert each value back to its corresponding original one. In this case, list 'a a a' would give 6 identical permutations. Is that what you are looking for?
I'm pretty sure it can be done with [list-find] and [list-idx], I'll try and update the patch in the next few days.
-
Some slight modifications with [list fromsymbol] and [list tosymbol]. This should now work for lists of floats like 1 2 3 and symbols like abc, but not for lists of symbols like a b c.
Heaps_algorithm2.pd -
@weightless the list could be made of integers, one integer would represent a percentage of the volume of a harmonic, or maybe it can be done directly with the percentage numbers (its just easier for me when doing the permutations manually to think of letters), so it would be like this simply with three percentages for three harmonics, how about, initially, harmonic "a" or "1" would have its volume at 34%, harmonic b or 2 at 67%, and harmonic c or 3 at 100% (At the end I want to go all out on this morphing timbre exercise and implement 32 harmonics for maybe 10 or 32 volume percentages, if there are 32 harmonics and 10 volume percentages there would have to be repetitions or maybe 64 harmonics and 100 different volume percentages!).
I think that what is more difficult to grasp here are the repetitions, the permutations are done, we understand that three different elements would have 6 permutations (I checked out your randomize patch, nice, i was thinking of that also, for an option to randomize the list if you wanted of all possible combinations with their repetitions), I think of the repetitions like this: first you have to know how many harmonics you have, and how many percentages you will have , so let´s say three harmonics "A""B""C", and three options for percentages a=34%, b=67% and c=100%, so its three to three options.
The first category would be for there to be one repetition, (so two equal letters), so we start with first harmonic at 34% , second at 34% and third at 67%, Im going to use only letters now for the percentages, so that was a,a,b. then it´s permutations (a,b,a; b,a,a), now same category but "a" against "c" so: aac, aca,caa
then once we have already past letter a against all possible letters in order we go to another category (three equal letters) "aaa", then we are done with "a", now we go back to the first category (one repetition) but we start with the second letter "b", so now its bba, bab,abb, then bbc,bcb,cbb then bbb, then cca, cac, acc, then ccb,cbc,bcc then ccc, now, i think those are all possible repetitions with 3 harmonics. So when the curve in iannix is at the top that means start the list with with different elements (3 harmonics, 6 permutations), then the repetitions (21 combinations). or maybe an option to start first with the repetitions then with the different elements
-
@weightless If [until] crashes Pd, that usually means that it never gets a bang to its right inlet. You have to make sure that it gets that bang, and still better always save your patches before testing anything involving [until].
 At least that's how i do it.
At least that's how i do it. -
@Pándinus This could be a source of inspiration for your task: https://rosettacode.org/wiki/Permutations_with_repetitions.

-
@ingox Thanks!
-
@ingox Ill send this page to my teacher, who is helping me with this
-
This should generate all possible combinations of elements of a symbol or a list. Elements will also be combined with themselves.
The number of all combinations is n^n. On my computer it worked with a list of six elements, but crashed Pd with a list of seven.
Input: abc
Output: aaa, aab, aac, aba, abb, abc, aca, acb, acc, baa, bab, bac, bba, bbb, bbc, bca, bcb, bcc, caa, cab, cac, cba, cbb, cbc, cca, ccb, ccccombinations.pd (old)
combinations-help.pd (old)It basically just counts up in an n-ary numeral system, n being the length of the list.
-
This version generates every combination directly from the previous one and is therefor in theory only limited by computer memory. On my computer it generated all 823543 combinations of 1 2 3 4 5 6 7 within a few minutes.
It can output the results in variable length, which can be set via creation argument or right inlet. If no length is provided, the results will have the same length as the original.
-
Input: abc
Output of [combinations]:
aaa, aab, aac, aba, abb, abc, aca, acb, acc, baa, bab, bac, bba, bbb, bbc, bca, bcb, bcc, caa, cab, cac, cba, cbb, cbc, cca, ccb, ccc -
Input: abcd
Output of [combinations 2]:
aa, ab, ac, ad, ba, bb, bc, bd, ca, cb, cc, cd, da, db, dc, dd -
Input: ab
Output of [combinations 4]:
aaaa, aaab, aaba, aabb, abaa, abab, abba, abbb, baaa, baab, baba, babb, bbaa, bbab, bbba, bbbb
The right outlet sends a bang when the generation is complete.
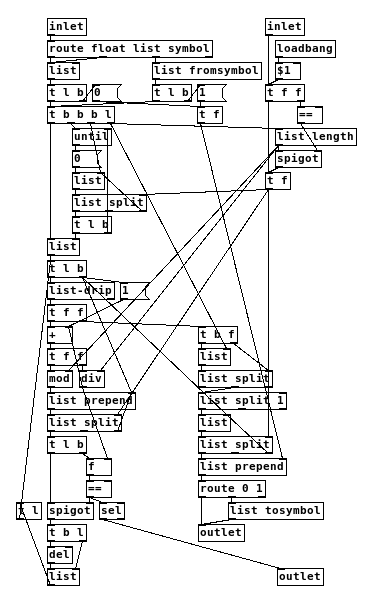
combinations.pd
combinations-help.pdHow it works:
Internally, the patch uses lists of numbers 0, 1, ..., n-1; n being the length of the original list. These numbers serve as digits of an n-ary system. It starts with a list of zeros. The digits of each list are send to the right branch (output) and the left branch (iteration) of the patch.At each iteration, one is added to the first digit of the list. If the result equals n [mod] sets it to zero and [div] takes the carry-over (1) to the next digit. If there is still a carry-over after the last operation, meaning that the current combination is the last one, the spigot is closed and it stops.
Before the output, the internal digits of each list are replaced with the numbers or symbols of the original list. Zero is replaced with the first element, one with the second and so on.
After each iteration a delay 0 is used to brake the loop and avoid stack overflow.
Uses [list-drip] from list-abs extension.
-
-
@ingox Thanks for sharing this patch, it looks like it does exactly what I was hoping to achieve with my patch but in a much more elegant and versatile way, so I think I'll abandon my attempt!
-
@ingox your patch is great, and generates the sequence just how i pictured it, but now how do I apply it in iannix? this is the score i made with iannix...DS3.iannix , each pink curve represents pitch and the other colored curves are for morphing timbre, there are 31 pink curves and another 31 green ones or whatever that color is... each green one will control the timbre of an individual pink one...
how do I apply your patch with the iannix score? there will be 8 harmonics with 4 different positions in volume each for a start (25%, 50%, 75% and 100%), and the change has to be continuous, if the curve is continuous; If its rectangular at any point and cuts off instantly there will be a jump from timbre to timbre.