I'm new to Pd and going through the official tutorial. And I'm am overcome by the complexity of the proposed solution to the first exercise, "2.2.1.2.7 Random without repetitions".

More precisely, I'd like to know why such complexity? Why would my attached patch cause problems?

Thanks in advance for your insights

Hi and welcome to this forum,

As far as I can tell, there is absolutely nothing wrong with your solution, and that is quite a clever way to solve this problem! About your question, keep in mind that often there are many ways of implementing a same algorithm, or a different one that does the same thing, in Pd (or rather in programming in general). Sometimes people may miss a shorter solution, or may select a longer one for other reasons (for the sake of clarity, for instance, or for using only "vanilla friendly" objects, or maybe the solution is an adaptation of another algorithm created for a different purpose, etc.).

Hope this helps, take care!
Gilberto

Now try writing it in a way that uses a constant number of operations each time.

Got a candidate:

random-no-contiguous-repeats-in-constant-time.pd

@jancsika that's quite a nice solution! I did check that it is in fact uniformly distributed -- as expected --, but I feel quite uneasy about using a pseudorandom number generator producing N-1 integers for spitting out N integers by simple means of addition and module operation. Are you sure there are no undesirable side effects to this method? See for instance this page here: https://en.wikipedia.org/wiki/Pseudorandom_number_generator#Potential_problems_with_deterministic_generators

Also, out of curiosity, which situations would require an abstraction to use a constant number of operations? Or did you approach this more as a challenge?

Cheers!
Gilberto

I'm not certain there aren't side-effects. But it's difficult to conceive how there could be a side-effect that wouldn't also affect the other two solutions.

I think it's a useful challenge for a realtime audio environment. Theoretically, the first two solutions might never return. Practically, they might use more CPU than one would guess, especially if they end up in a large number of abstractions sprinkled throughout a larger program.

But it's difficult to conceive how there could be a side-effect that wouldn't also affect the other two solutions.

I don't think this is difficult to conceive. The first solutions are simple: you bang again the [random] object if there is a repetition. Therefore all numbers are still produced by that PRNG, it's just that we choose to ignore the ones that do not fit our problem. In your case, as I pointed out, you are attempting to generate N+1 non repeating random numbers from and input of N random numbers, and this sounds fishy to me. Mapping down is easy, e.g. if we have a generator producing numbers between 0-7 and we want only 0s or 1s, we can map it such as that 0-3 => 0 and 4-7 => 1. But the opposite is not possible with direct mapping. You could of course then group every three results, such as that 000 => 0, 001 => 1, 010 => 2, ... 111 => 7, but I don't see how a similar solution could be achieved using just sum and modulo operators, so I suspect your results might have some side effects.

Cheers!
Gilberto

@gsagostinho: Ok. Thanks! So I'll have to ask Johannes Kreidler what was intended in the solution he provided.

PS: New version of randiff.pd with a slight change to centralize initialization.

@jancsika: I'm no expert of RT audio but, first, as the number generation is (here) the result of a manually generated event, I cannot see why a few clock cycles would matter timing-wise ; second, the chance these solutions never return exist but are really low, eg: with random 5, not getting a new number out of 4 possibilities in 10 tries is already a 1ppm event! Pd is for me about livecoding, so I prefer to go with easy to code blocks and manually edit something in case of need. That's why I was perplexed by the complexity of the original solution.

But the smaller the limit number, the more likely it is you will get repeat numbers, and hence the less efficient this method becomes. If you choose [random 2], there is a 1/1024 chance that you'll get 10 in a row, which is not negligible. And if you take it to the absolute limit and make [randiff 1], you're going to get a stack overflow because it will always choose and then reject 0.

Here is a hybrid solution. random-hybrid.pd

If the number is rejected, it adds and wraps another random number, maximum n-1. That way it will never take more than 2 cycles, but also avoids the un-even distribution that Gilberto is worried about.

@cmnmnum Johannes Kriedler does have a peculiar patching style, and many of those examples can be made more efficient. I still have a lot of respect for the man though!

@gsagostinho I'll have to think about that one a bit more...

@cmnmnum You're right that in the manually-triggered example the extra cycles are unlikely to matter. I'm just thinking of situations where that functionality is made general inside an abstraction. Then the code could be used in many different contexts-- it its used rapidly to generate many random values while audio is running the cycles could become important. (Especially if one employed many copies of the abstraction in a more complex patch.)

@gsagostinho Do you mean that someone using my abstraction as a model could easily lead to unintended side effects, or are you saying that the abstraction itself has side-effects which the first two approaches do not?

@jancsika I mean that the model could have unintended side effects. Supposing these side effects exist, they might be noticeable or not depending on what you use the pseudorandom numbers for. For instance, generating 20 numbers in order to select random chords for a composition very likely won't give you enough data to see side effects, but if you generate a million of them then you might spot something. Any PRNG should output numbers that are uniformly distributed, and as I mentioned to you your abstraction does do that correctly, but there are other characteristics that can be observed, for instance the presence of patterns in the output.
For instance, PRNG do cycle back and start outputting the same series of numbers again in the same order, and the larger these cycles (periods) are the better a generator is. If you think about it, a simple counter does fulfil the uniform distribution requirement, but those "random" numbers it output will be very poor given that they have a short cycle of repetition (e.g. 0 1 2 0 1 2 0 1 2). On the other hand, the RANDOM_NUMBER subroutine in Fortran has a period of 2^1024 - 1 (aprox. 10 to the 308 power), and so that is an excellent period size. And then there are other types of side effect that could be observed (see for instance https://en.wikipedia.org/wiki/Pseudorandom_number_generator#Potential_problems_with_deterministic_generators ).

@LiamG

That way it will never take more than 2 cycles, but also avoids the un-even distribution that Gilberto is worried about.

To be precise, I do think that solution is uniformly distributed as I checked it for very large numbers, my worries is concerning other side effects. I just can't wrap my head around the idea of using N input numbers to generate N+1 output numbers without side effects.

@gsagostinho I'm going to go ahead and claim that they are functionally equivalent. But if I'm wrong I'd love to see a demo showing the side-effect.

@jancsika

I'm going to go ahead and claim that they are functionally equivalent.

Well, a claim like this does not bring much to the table, does it?

But if I'm wrong I'd love to see a demo showing the side-effect.

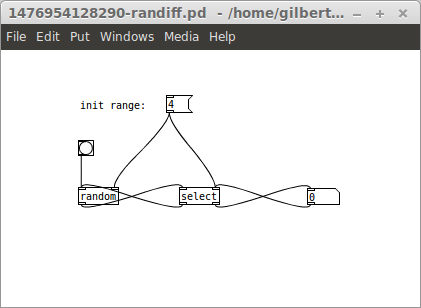
I think I found just that. I created a large number of outputs from your algorithm and analysed it for patterns that shouldn't be there. So even if the output of a PRGN does obey a uniform distribution, it will still be weak if it show certain patterns (remember, randomness is the lack of patterns). I calculated the frequency of every string of size 4 output by your algorithm, and the results display a quite non-random behaviour. See, there are 4×3×3×3 = 108 possible strings of size 4 of non-repeating numbers (4 options for the first position, 3 for the second position since it can't repeat the previous, 3 again for the third position since it can't repeat the value of second position and 3 for the last position for the same reason). So it means that any string of 4 numbers should appear 1/108 = 0.009259259 = 0.9 % of the time. What I found out is that your algorithm is not able to output any sequence of four digits in which every digit is unique (e.g. {0,1,2,3}, {3,1,0,2}, {2,0,1,3}, etc.). If out of those 108 possibilities we remove the 24 that are made out of unique numbers (4×3×2×1 = 24), we then have 84 options. And indeed all other strings appear 1/84 = 0.011904762 = 1.2% of the time each. This shouldn't be a characteristic of a PRNG.

I then took a quick look at strings of size 3. I found that several strings do not appear either, such as {0,1,2}, {2,3,0}, {3,0,1}, {0,1,0}, {0,2,0}, and so the ones that appear do it much more frequently than they are supposed to. In fact, I believe that this behaviour will be present in strings of any size. And I am quite certain that this is a side effect of the mapping I mentioned before.

Hope this helps, cheers!
Gilberto

@LiamG and in that case, I suspect your hybrid algorithm above will also have some undesirable side effects.

@gsagostinho said:

@jancsika

I'm going to go ahead and claim that they are functionally equivalent.

Well, a claim like this does not bring much to the table, does it?

True.

Suppose that instead of trying again on contiguous repetitions the original patch instead used [random 10] and tried again for all outputs between 2 and 9.

Ignoring the cpu usage, is the output of such a patch functionally equivalent to [random 2] or not?

@jancsika I believe so, because a good PRNG is trying to emulate true randomness, and true random events are not affected by previous or future events.

This is why the approach of ignoring repetitions by [random] might be better, since a repeated number is simply ignored, and the chance of having {0,0} is the same as {1,1} or {2,2} etc., and so no pattern is introduced.

@gsagostinho said:

@jancsika I believe so, because a good PRNG is trying to emulate true randomness, and true random events are not affected by previous or future events.

Ok.

Is a revised version of OP's patch where N = 2 equivalent to [random-no-contiguous-repeasts-in-constant-time 2] or not?

Edited: originally compared to [random 2] which is wrong

@jancsika

Is a revised version of OP's patch where N = 2 equivalent to [random-no-contiguous-repeasts-in-constant-time 2] or not?

Sorry but I do not understand, which version of the OP's patch are you talking about? This one here?

And if so, I do not understand what you want to compare it to (I got confused by what you mean with the [random-no-contiguous-repeasts-in-constant-time 2] ).