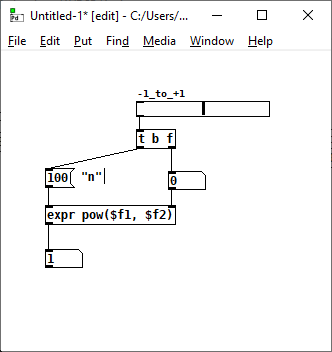
I'm trying to solve the maths behind the lin to log conversion in the sliders properties:
- Give a log slider a (0.1-10) range, and its centre position will be equal to 1
- Give a log slider a (0.01-100) range, and its centre position will still be 1
This is a great behavior for pitch scaling when you want to create a frequency offset of an oscillator in relation to another. For instance, with a (0.1-10) range, you get unison at centre position, +10 octaves at max position and -10 octaves at min position.
I want to recreate a similar behavior by converting a positive signal ranging (0 to n) linearly to a signal ranging (1/n - n) logarithmically.
The function should be something like this I believe:
f(0) = 1/n
f(n/2) = 1
f(n) = n
Did a bit of research and I think the function should look something like: y = a exp (bx).
My maths is a bit rusty I'm afraid. Could you help me solve this problem?

 I'm assuming you're like me in that you enjoy figuring stuff out for yourself, but it's OK if I'm wrong)
I'm assuming you're like me in that you enjoy figuring stuff out for yourself, but it's OK if I'm wrong)