Hello,
In "Designing Sound" by Andy Farnell, p. 378-379, he gives the following description of how to approximate the resonance duration of bells inside of a telephone box:
Making a Box
The resonator in figure 29.14 sends its input signal into two delays that feedback into each other. Between them is a fixed filter that mimics the material properties of the box and a that serves to limit the signal and introduce a little distortion to create a brighter sound. An old telephone has a box about 20cm to 30cm (12 inches) square. From the speed of sound being 340m/s we get a resonance of 0.3/340ms or about 1.1kHz. Two delays are used with the length being slightly longer than the width. Tapping some Bakelite shows resonances somewhere between a hard wood and plastic, and for a plate about 5mm thickresonances were seen at 1kHz, 500Hz, and 300Hz. Choosing the exact values for the patch in figure 29.14 requires a bit of tweaking by hand. You want to find two values for the acoustic resonance and set the width, length, and feed-back to give a good effect, while at the same time you must pick filter valuesthat give a nice hollow radiated tone. Picking feedback values close to 0.7 givesgood results; then tune the filters to get the quality of a plastic box without accidentally sending the acoustic resonator into unstable feedback.
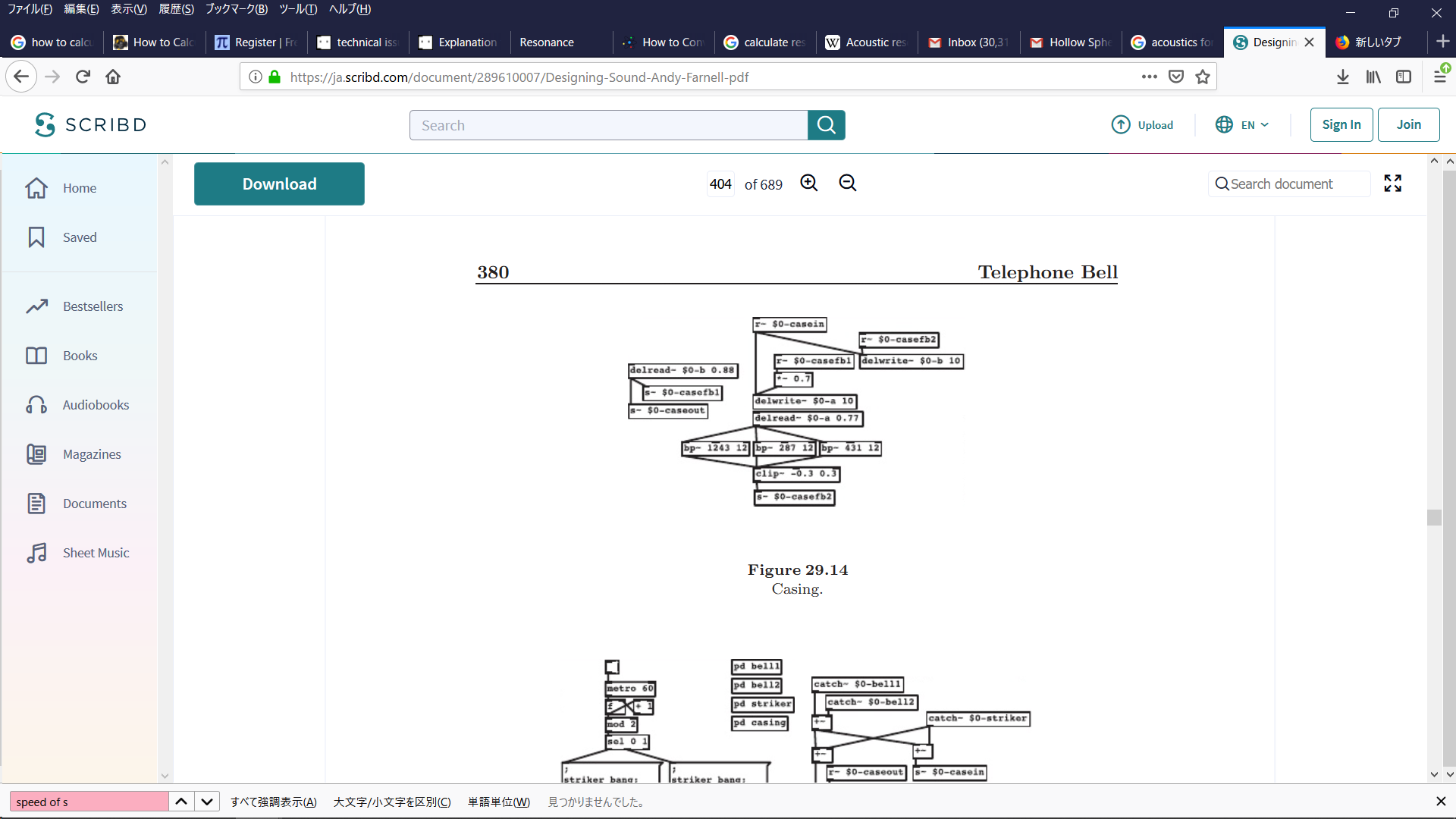
Now, I understand that 0.3/340ms = 1133Hz (about 1.1kHz) and 1/1133 = 0.88ms which is the value he used for one of the delays in his "casing" patch. What I don't understand is how he got the resonance value of 0.3/340ms to begin with. I assume the 0.3 comes from the 30 centimeters, ie. the width of the box, but what about the 340 ms? It looks related to the speed of sound, but how exactly? And is this a formula I can reuse, ie.
w/340 = r
where w is the width in meters and r is the resonance frequency in Hertz? I tried Googling this but the resonance formulae that came up were much more complex.
Also, apologies if this topic is less about PD and more about Math/Acoustics. In the future, would it be better to ask questions like this on a math forum instead?



 and/or do the stuff in the helpfiles G04.control.blocksize.pd and G05.execution.order.pd where you can
and/or do the stuff in the helpfiles G04.control.blocksize.pd and G05.execution.order.pd where you can