Hello,

When I use [writesf ~] and I send "stop" with a low delay time (as in the photo) it doesn't record me respecting the indicated time. (about 3.6 ms ahead) If the sample should last 35.19274376, the end result is 34.82993197 ...

This becomes a serious problem for me because I cannot work the way I would like.

If I record the contents of a table with [soundfiler], the problem disappears, but I have not been able to record at 24bit (as with [writesf ~])

I would like them to tell me what I am doing wrong and how I could solve it.

Thank you!!

By default, Pd calculates in blocks of 64 samples.

Control messages like "stop" may occur only between blocks... meaning that you don't have sample-accurate control over starting and stopping the recording.

With a 64 sample block and a 44.1 kHz sample rate, the block duration is 64/44.1 = 1.45125 ms.

35.19274376 / (64/44.1) = 24.25, including a quarter of a block.

34.82993197 / (64/44.1) = 24.0, truncated to the previous block boundary. That's not a coincidence.

You might be able to get sample accurate control by putting the recorder in a subpatch with a [block~] object setting the block size to 1, but I'm not certain it'll help your case (haven't tried it myself).

hjh

@EMR66 As above.
For [tabread4~] the table should be 3 samples longer as it is interpolating.... see the help file.
That could explain the truncation to the previous block boundary.

But you should be able to record at a 24 bit depth from [soundfiler] with the message [write -bytes 3 Ak1.wav(
Although I don't know why you would want to do that.
16 bits is enough.
Pd is 32 bit floating internally and will write that with a -bytes 4 command which will keep all information....... and give higher resolution at smaller amplitudes........ and preserve 24 bits if that was what was actually captured by an adc.
Of course the table will not be true 32 bit floating if the source was 24 bit......... but the output from [tabread4~] will be a 32 bit representation of it by interpolation.
But you don't gain anything by interpolation before writing. If you want to preserve the original file you should use [tabplay~] or you are just introducing quantization (errors) that are functional for a dac or varispeed (up/downsampling) but not for a file.
24 bit is actually 23 bits and the sign for amplitudes between -1 and 1.
Our hearing is 14 bit.
David.

Agree!!

Thank you very much to the 2 for the answers!

A greeting!!

Hello,

I still have the same problem recording. I cannot achieve maximum precision with PD.

For example:
If I record the contents of a table containing a 1Hz sine wave, with a table size of 44100 samples, [soundfiler] records the 44100 samples perfectly (1000ms).

But if I want to record an 8Hz wave (5512.5 samples) (125ms), the table will only accept 5512 samples, (124.988..ms)

This time difference may seem insignificant, but for my work it is becoming a horror.

You have advised me to use [writesf ~] in an subpatch with [block ~ 1] but I don't know exactly how to do it. (Sometimes I learn better with an image than in writing) and I have not seen clear examples of [block ~] in the help file.

Any ideas? Thank you!!

although it would not solve it either, since the "stop" message would only work from sample to sample, and not between samples, right?

@EMR66 We don't know what you are trying to achieve with your patch.
No digital audio can have a "half" sample. You will need to double the sample rate to record one complete 8Hz wave.
Here is a better help file for [block~] from the old extended version of Pd...... block~-help.pd but as you will see it allows processing at a block size of one sample....... which will not help you.

But it does also allow up and down sampling so you could use [writesf~] in a sub-patch with [block 4096 1 2] to write at 88200 unless [writesf~] writes the file header at the sample rate fixed by the Pd media settings........ in which case you will have to set Pd to 88200 and use [writesf~] without block.

It will be interesting to know.
David.

@EMR66 "But if I want to record an 8Hz wave (5512.5 samples) (125ms), the table will only accept 5512 samples, (124.988..ms) This time difference may seem insignificant, but for my work it is becoming a horror."

It's also, as David said, a wrong conception.

There is no such thing as a fractionally-sized wavetable. Period, full stop. (That's the main reason why you haven't been able to write exactly the duration you want: because it's impossible.)

The only way to use a wavetable to generate a frequency that is not an integer number of samples is to play back the wavetable with interpolation. (EDIT: David's solution (make the wavetable twice as long, and read every other sample) is also valid -- a different way around to the same result. I overstated a bit to say "the only way.")

You'll simply have to make the wavetable with an integer size (plus an extra 3 samples, per tabread4~'s requirement) and play it back at the desired rate, and allow tabread4~ to do its job and interpolate the samples for you.

hjh

t was impossible for me to record with [writesf ~] respecting the actual duration. (I can't even get to record 44100 fair samples)

I don't know if I use [block ~] incorrectly, but at the moment I have only got a real precision, using soundfiler (although this limits me since the table only accepts whole samples as we have already spoken ..) So, until I get that [writesf ~] record correctly, it is useless for me to use [tabread4 ~] or [tabplay ~] ...

By changing the frequency to 88200, (both Pd's and my interface's) and trying to draw waves on a table with [tabwrite ~], for some unknown reason, Pd crashes me ..

So I will leave it for the moment and I will return to the problem again later.

Thank you!! Greetings!!

@EMR66 "I have only got a real precision, using soundfiler (although this limits me since the table only accepts whole samples as we have already spoken ..)"

This, of course, is not a limitation of soundfiler... It's a limitation of all sampled audio files.

There is no way to create an audio file, in any software, containing a fractional number of samples. Period, end of discussion.

In theory, if the frequency is a rational number, you could find the least common multiple of the wavelength and 1.0 and then have all the required sample values precalculated. But this would disallow irrational wavelengths because the LCM would be infinite. So if the desire is to support every possible real number frequency, without interpolation, it's mathematically impossible because of irrational numbers.

To handle every possible real number frequency requires interpolation. There is no way out of that.

"So, until I get that [writesf ~] record correctly, it is useless for me to use [tabread4 ~] or [tabplay ~] ..."

A fractionally sized wavetable is impossible. Literally, impossible.

Meanwhile, it's very easy to play a wavetable at an arbitrary frequency, with interpolation.

The practical solution here is to create the wavetable with a whole number of samples and interpolate in the wavetable oscillator.

hjh

@EMR66 As explained, you will never be able to write an audio file at a precise length without changing the sample rate for each and every wave frequency.
[writesf~] is working correctly but your requirement cannot be satisfied (in any software..... see above).

If your requirement for a precise (time length) of file is for some purpose outside of Pd then you will never solve your problem.

If you read the file back into Pd (or any other software) it can be interpolated and play correctly.
It will also be possible to analyse the wave, as it is a single frequency, and print the time that you expect.
Pd is maybe the only software that would make that solution fairly easy to program.

But if you expect to write an audio file of a calculated precise length for every possible frequency then you will have to change the sample rate for every frequency and they will all have to be resampled for playback which will impact sample precision.

So once again, what is the purpose of your required "precise" length of file?
There will probably be a way to achieve the same thing, but writing an audio file of "precise" duration will not be possible and you are wasting effort trying to do so.......

David.

Hi

It is not easy for me to explain why I need maximum precision, either because of the complexity that would be explained to me and because my English is not entirely good. Although if I can try to explain a simple example (although it is far from the real purpose)

Suppose I have 2 audio samples. The first sample lasts exactly 1000ms (44100 samples) and I loop it every 1000ms.

If I had another exactly 125ms sample and looped it back at its exact time (125ms) alongside the first 1000ms sample, the beat would be perfectly in sync since it's the exact eighth part of 1000.

On the other hand, if I can only get a sample of 5512 samples (124.988..ms) and I loop it along with the 1000ms sample, as time progresses and the 124.988 sample is repeated more times ... ms, the desynchronization of time will increase ... (rhythm)

I know you can tell me that I can solve the "desynchronization" by repeating the sample every exact 125ms, but I have already said that this is just a simple example to try to explain and does not address the real problem.

As I have understood from your explanations, that sometimes it will be impossible for me to record samples to the exact duration that you want, but I can reproduce them within Pd exactly with the desired duration using the examples that you have given me. What invites me to think about the idea of ​​not using any other means than Pd to get closer to my purpose, even if it takes more time and effort at first; But it is what I will do ..

Thank you

A greeting!!

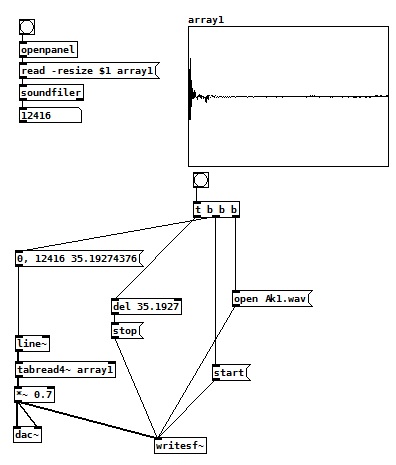
@EMR66

A couple of illustrations.

Let's say we want a sine wave covering 16.5 samples. To illustrate, I used SuperCollider to put two sine wave cycles into 33 samples.

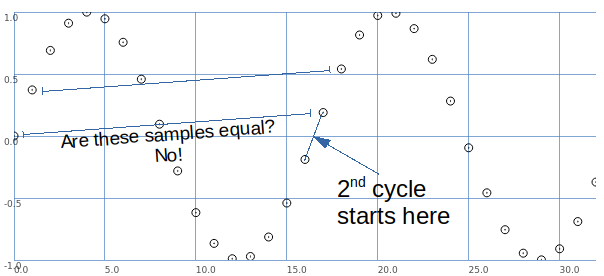
The second cycle begins when the wave crosses the 0 line in the middle.

This is between samples.

So, the second cycle must be represented by sample values that are different from the sample values for the first cycle.

That is, it is possible to have that zero crossing between samples -- but the sampling process produces different values.

Let's look at it a different way: blue samples = one sine wave cycle covering 33 samples; green samples = 2 cycles in 33 samples.

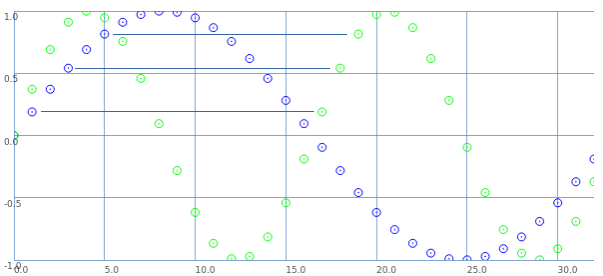
If we start counting samples at 0:

• Blue 0 = Green 0.
• Blue 2 = Green 1.
• Blue 4 = Green 2. etc.

That is: read through the blue samples at double speed, and you get the 16.5 wavelength. (This is exactly what David said.)

What about the second cycle starting at 16.5?

• Blue 1 = Green 17.
• Blue 3 = Green 18. etc.

These are the sample values that were skipped the first time.

So, Green 17 (the first concrete sample value after the second cycle begins) is the value in between Green 0 and Green 1. Green 18 is in between Green 1 and Green 2.

This is interpolation.

Interpolation is the mathematically correct way to represent fractional cycles in a sampled signal.

You can try to say that this "isn't the real problem," but... this is the problem, and interpolation is the solution.

hjh

Now I see it even clearer !!
Thank you very much for the help and for your time !!

A greeting!