In mathematics, a Hilbert transform can be used to synthesize the imaginary part of a real signal, thereby providing the part needed to make it a complex-valued signal. Complex-valued signals are useful because you can among other things know the amplitude from a single sample. [hilbert~] is a fast approximation using all-pass filters but is not quite the same because it also phase-shifts the original real valued signal. This demonstration was inspired by Katja V's discussion and was greatly improved using info from @Nicolas-Danet. Select each of the three phase comparisons in turn and graph their respective phase shifts to see how the hilbert~ magic is performed.

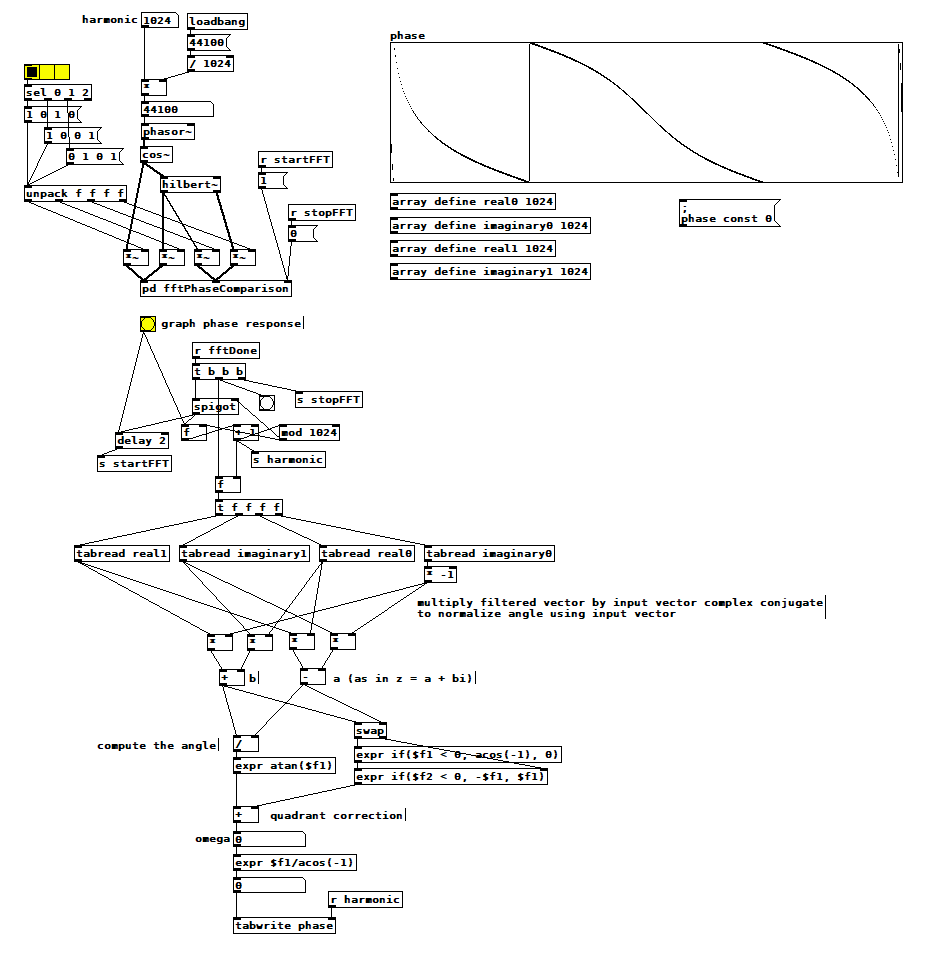
hilbert~ phase.pd

Thanks, it makes me want to read the Katjaas's blog!

I was wondering if I could test all the FFT frequencies at once, so I started painstakingly building a 1024 pt wave table with all the harmonics in it, and then I saw it <gasp>: it's just the impulse function. I've read about that equivalence a hundred times, but it never sank in until just now. Two and a half days of thrashing around, worrying about [switch~], [bang~], reblocking, vector discontinuities....ok, it was interesting, but completely unnecessary!
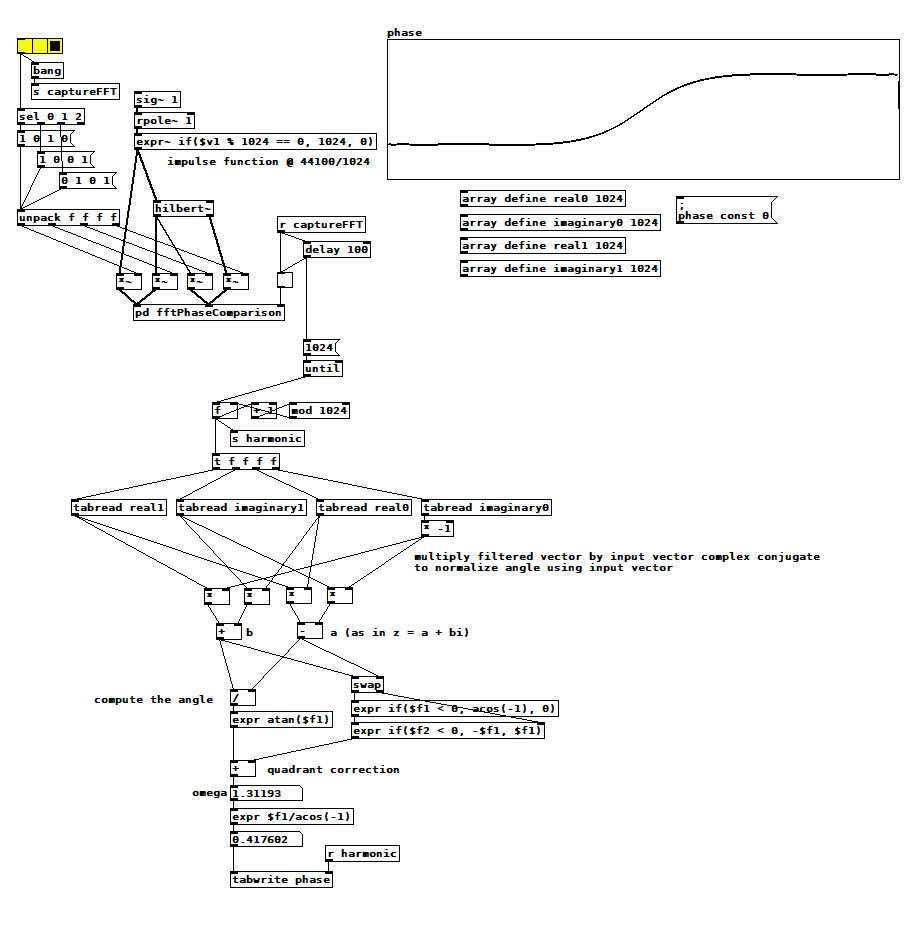hilbert~ phase2.pd

Archimedes @jameslo

@whale-av Well, that metaphor applies only if, prior to taking his bath, Archimedes was told a hundred times to try putting the crown in a bucket of water.