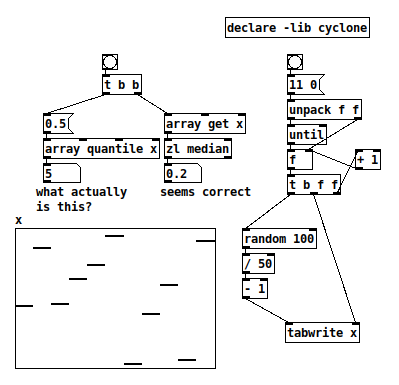
Does anybody know what the left inlet, and only outlet, of [array quantile] represent?
The left inlet is supposed to be 0.0 - 1.0, which I assumed to be a proportion. That is, I had guessed that 0.5 --> [array quantile x] would return either a value where half the array elements are below and half above, or the index whose value meets the same criterion.
This appears not to be the case.
For example, given array values (from a concrete test):
-0.1 0.72 -0.08 0.28 0.48 0.9 -0.94 -0.22 0.2 -0.88 0.82
0.5 --> [array quantile x] returns 5 (in other tests, it returned 2, 3, 7... so it isn't just half the array size). Assuming array indexing begins at 0, this points to 0.9.
Sorting the values gives:
-0.94 -0.88 -0.22 -0.1 -0.08 0.2 0.28 0.48 0.72 0.82 0.9
... whereupon we find that 0.9 is the largest value in the array...?
So I'm quite puzzled. The help file says "for instance, the 0.5 quantile is the median of the array" (which should be 0.2) but this does not line up with any concrete result I have been able to obtain.
hjh