@jancsika
I'm going to go ahead and claim that they are functionally equivalent.
Well, a claim like this does not bring much to the table, does it? 
But if I'm wrong I'd love to see a demo showing the side-effect.
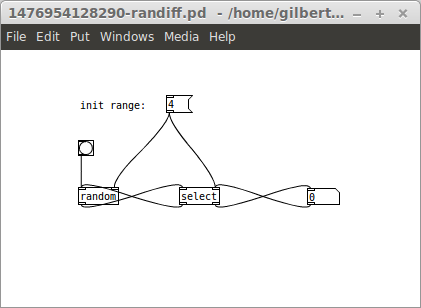
I think I found just that. I created a large number of outputs from your algorithm and analysed it for patterns that shouldn't be there. So even if the output of a PRGN does obey a uniform distribution, it will still be weak if it show certain patterns (remember, randomness is the lack of patterns). I calculated the frequency of every string of size 4 output by your algorithm, and the results display a quite non-random behaviour. See, there are 4×3×3×3 = 108 possible strings of size 4 of non-repeating numbers (4 options for the first position, 3 for the second position since it can't repeat the previous, 3 again for the third position since it can't repeat the value of second position and 3 for the last position for the same reason). So it means that any string of 4 numbers should appear 1/108 = 0.009259259 = 0.9 % of the time. What I found out is that your algorithm is not able to output any sequence of four digits in which every digit is unique (e.g. {0,1,2,3}, {3,1,0,2}, {2,0,1,3}, etc.). If out of those 108 possibilities we remove the 24 that are made out of unique numbers (4×3×2×1 = 24), we then have 84 options. And indeed all other strings appear 1/84 = 0.011904762 = 1.2% of the time each. This shouldn't be a characteristic of a PRNG.
I then took a quick look at strings of size 3. I found that several strings do not appear either, such as {0,1,2}, {2,3,0}, {3,0,1}, {0,1,0}, {0,2,0}, and so the ones that appear do it much more frequently than they are supposed to. In fact, I believe that this behaviour will be present in strings of any size. And I am quite certain that this is a side effect of the mapping I mentioned before.
Hope this helps, cheers!
Gilberto


 About your question, keep in mind that often there are many ways of implementing a same algorithm, or a different one that does the same thing, in Pd (or rather in programming in general). Sometimes people may miss a shorter solution, or may select a longer one for other reasons (for the sake of clarity, for instance, or for using only "vanilla friendly" objects, or maybe the solution is an adaptation of another algorithm created for a different purpose, etc.).
About your question, keep in mind that often there are many ways of implementing a same algorithm, or a different one that does the same thing, in Pd (or rather in programming in general). Sometimes people may miss a shorter solution, or may select a longer one for other reasons (for the sake of clarity, for instance, or for using only "vanilla friendly" objects, or maybe the solution is an adaptation of another algorithm created for a different purpose, etc.).


 ).
).